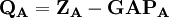Mulliken population analysis

Mulliken charges arise from the Mulliken population analysis and provide a means of estimating partial atomic charges from calculations carried out by the methods of computational chemistry, particularly those based on the linear combination of atomic orbitals molecular orbital method. If the coefficients of the basis functions in the molecular orbital are C_μi for the μ'th basis function in the i'th molecular orbital, the density matrix terms are:

$\mathbf {D_{\mu\nu}} = \mathbf{2}\sum_{i} \mathbf {C_{\mu i}} \mathbf {C_{\nu i}^*}$

Additional recommended knowledge

Weighing the right way

Guide to balance cleaning: 8 simple steps

Daily Visual Balance Check

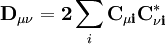
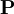for a closed shell system where each molecular orbital is doubly occupied. The population matrix $\mathbf{P}$ then has terms

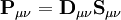
$\mathbf {P_{\mu\nu}} = \mathbf {D_{\mu\nu}} \mathbf {S_{\mu\nu}}$

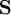$\mathbf{S}$ is the overlap matrix of the basis functions. The sum of all terms of 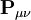$\mathbf {P_{\mu\nu}}$ is N - the total number of electrons. The Mulliken population analysis aims first to divide N among all the basis functions. This is done by taking the diagonal element of 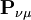$\mathbf {P_{\mu\nu}}$ and then dividing the off-diagonal elements equally between the two appropriate basis functions. Since the off-diagonal terms include $\mathbf {P_{\mu\nu}}$ and $\mathbf {P_{\nu\mu}}$ , this simplifies to just the sum of a row. This defines the gross orbital population (GOP) as

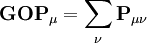
$\mathbf {GOP_{\mu}} = \sum_{\nu} \mathbf {P_{\mu\nu}}$

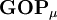The $\mathbf {GOP_{\mu}}$ terms sum to N and thus divide the total number of electrons between the basis functions. It remains to sum these terms over all basis functions on a given atom A to give the gross atom population (GAP). The sum of 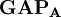$\mathbf {GAP_{A}}$ terms is also N. The charge, 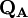$\mathbf {Q_{A}}$ , is then defined as the difference between the number of electrons on the isolated free atom, which is the atomic number 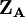$\mathbf {Z_{A}}$ , and the gross atom population:

$\mathbf {Q_{A}} = \mathbf {Z_{A}} - \mathbf {GAP_{A}}$

The problem with this approach is the equal division of the off-diagonal terms between the two basis functions. This leads to charge separations in molecules that are exaggerated. Several other methods have used to estimate atomic charges in molecules.

Mulliken population analysis

Additional recommended knowledge

Weighing the right way

Guide to balance cleaning: 8 simple steps

Daily Visual Balance Check

See also

References

About chemeurope.com

About LUMITOS

Advertise with LUMITOS