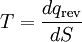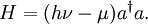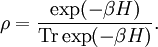Negative temperature

In physics, certain systems can achieve negative temperatures; that is, their thermodynamic temperature can be of a negative quantity. Negative temperatures can be expressed as negative numbers on the kelvin scale.

Temperatures that are expressed as negative numbers on the familiar Celsius or Fahrenheit scales are simply colder than the zero points of those scales. By contrast, a system with a truly negative temperature is not colder than absolute zero; in fact, temperatures colder than absolute zero are impossible. Rather, a system with a negative temperature is hotter than the same system with an infinite temperature.

Additional recommended knowledge

Daily Visual Balance Check

Weighing the right way

What is the Sensitivity of my Balance?

Heat and molecular energy distribution

Negative temperatures can only exist in a system where there are a limited number of energy states (see below). As the temperature is increased on such a system, particles move into higher and higher energy states, and as the temperature becomes infinite, the number of particles in the lower energy states and in the higher energy states becomes equal. (This is a consequence of the definition of temperature in statistical mechanics for systems with limited states.) By injecting energy into these systems in the right fashion, it is possible to create a system in which there are more particles in the higher energy states than in the lower ones. This situation can be characterised as having a negative temperature. A substance with a negative temperature is not colder than absolute zero, but rather it is hotter than infinite temperature. As Kittel and Kroemer (p.462) put it, "The temperature scale from cold to hot runs +0 K, . . . , +300 K, . . . , +∞ K, −∞ K, . . . , −300 K, . . . , −0 K."

Generally, temperature as it is felt is defined by the kinetic energy of atoms (heat). Since there is no upper bound on momentum of an atom there is no upper bound to the number of energy states available if enough energy is added, and no way to get to a negative temperature. However, temperature is more generally defined by statistical mechanics than just kinetic energy (see below).

Temperature and disorder

The distribution of energy among the various translational, vibrational, rotational, electronic, and nuclear modes of a system determines the macroscopic temperature. In a "normal" system, thermal energy is constantly being exchanged between the various modes.

However, for some cases it is possible to isolate one or more of the modes. In practice the isolated modes still exchange energy with the other modes, but the time scale of this exchange is much slower than for the exchanges within the isolated mode. One example is the case of nuclear spins in a strong external magnetic field. In this case, energy flows fairly rapidly among the spin states of interacting atoms, but energy transfer between the nuclear spins and other modes is relatively slow. Since the energy flow is predominantly within the spin system, it makes sense to think of a spin temperature that is distinct from the temperature due to other modes.

A definition of temperature can be based on the relationship:

(See here for discussion)

The relationship suggests that a positive temperature corresponds to the condition where entropy, S, increases as thermal energy, q_rev, is added to the system. This is the "normal" condition in the macroscopic world and is always the case for the translational, vibrational, rotational, and non-spin related electronic and nuclear modes. The reason for this is that there are an infinite number of these types of modes and adding more heat to the system increases the number of modes that are energetically accessible, and thus the entropy.

Examples

Nuclear spins

In the case of electronic and nuclear spin systems there are only a finite number of modes available, often just two, corresponding to spin up and spin down. In the absence of a magnetic field, these spin states are degenerate, meaning that they correspond to the same energy. When an external magnetic field is applied, the energy levels are split, since those spin states that are aligned with the magnetic field will have a different energy than those that are anti-parallel to it.

In the absence of a magnetic field, one would expect such a two-spin system to have roughly half the atoms in the spin-up state and half in the spin-down state, since this maximizes entropy. Upon application of a magnetic field, some of the atoms will tend to align so as to minimize the energy of the system, thus slightly more atoms should be in the lower-energy state (for the purposes of this example we'll assume the spin-down state is the lower-energy state). It is possible to add energy to the spin system using radio frequency (RF) techniques. This causes atoms to flip from spin-down to spin-up.

Since we started with over half the atoms in the spin-down state, initially this drives the system towards a 50/50 mixture, so the entropy is increasing, corresponding to a positive temperature. However, at some point more than half of the spins are in the spin-up position. In this case, adding additional energy reduces the entropy since it moves the system further from a 50/50 mixture. This reduction in entropy with the addition of energy corresponds to a negative temperature.

Semiconductor lasers

This phenomenon can also be observed in many lasing systems, wherein a large fraction of the system's atoms (for chemical and gas lasers) or electrons (in semiconductor lasers) are in excited states. This is referred to as a population inversion.

The Hamiltonian for a single mode of a luminescent radiation field at frequency ν is

The density operator in the grand canonical ensemble is

For the system to have a ground state, the trace to converge, and the density operator to be generally meaningful, βH must be positive semidefinite. So if hν < μ and H is negative semidefinite, then β must itself be negative, implying a negative temperature.

References

• Kittel, Charles and Herbert Kroemer (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 0-7167-1088-9. 
• Castle, Jack Jr. and Werner Emmerich and Robert Heikes and Robert Miller and John Rayne (1965). Science by degrees: Temperature from Zero to Zero. a Westinghouse Search Book by Walker and Company, New York. 
• Montgomery, David C. (1972-04-10). "Two-dimensional vortex motion and “negative temperatures”". Physics Letters A 39 (1): 7-8. doi:10.1016/0375-9601(72)90302-7.
• Edwards, Samuel F. and J. Bryan Taylor (1974-02-05). "Negative Temperature States of Two-Dimensional Plasmas and Vortex Fluids". Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences 336: 257-271.
• Hsu, Wenyue and Richard Barakat (1992-09-15). "Statistics and thermodynamics of luminescent radiation". Physical Review B 46 (11): 6760-6767. doi:0.1103/PhysRevB.46.6760.

Further reading

• Purcell, Edward M. and Robert V. Pound (1951-01-15). "A Nuclear Spin System at Negative Temperature". Physical Review 81 (2): 279-280. doi:10.1103/PhysRev.81.279.
• Ramsey, Norman F. (1956-07-01). "Thermodynamics and Statistical Mechanics at Negative Absolute Temperatures". Physical Review 103 (1): 20-28. doi:10.1103/PhysRev.103.20.
• Sitek, Ted. "ENTROPY–a root cause of Aging and the Widespread Fatigue Damage", Federal Aviation Administration USA, 2005, [1]

Recent applications

• Thermal Time Scales in a Color Glass Condensate
• Atomic Gases at Negative Kinetic Temperature
• Control of Local Relaxation Behavior in Closed Bipartite Quantum Systems
• Dark energy and supermassive black holes
• Anti-shielding Effect and Negative Temperature in Instantaneously Reversed Electric Fields and Left-Handed Media
• Minimax games, spin glasses, and the polynomial-time hierarchy of complexity classes[2]