To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Oscillator strengthAn atom or a molecule can absorb light and undergo a transition from
one quantum state to another. The oscillator strength is a dimensionless
quantity to express the strength of the transition.
The oscillator strength f12 of a transition from a lower state
Product highlightwhere me is the mass of an electron and The oscillator strength is the same for each sub-state Sum ruleThe sum of the oscillator strength from one sub-state
See alsoReferences
Categories: Spectroscopy | Atoms |
||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Oscillator_strength". A list of authors is available in Wikipedia. |


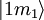 to an upper state
to an upper state 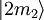 may be defined by
may be defined by
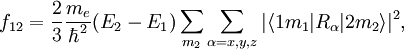



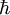 is
the reduced Planck constant. The quantum states
is
the reduced Planck constant. The quantum states 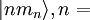 1,2, are assumed to have several
degenerate sub-states, which are labeled by
1,2, are assumed to have several
degenerate sub-states, which are labeled by 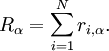
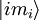 to all
other states
to all
other states 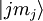 is equal to the number of electrons
is equal to the number of electrons 

