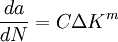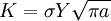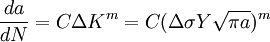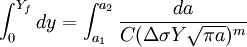To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Paris' lawIn materials science and fracture mechanics, Paris' Law is used to relate the stress intensity factor to subcritical crack growth under a fatigue stress regime. Product highlightWhere a is crack length, C and m are material constants, and ΔK is the stress intensity factor range. History and UseThis formula was generated from P.C. Paris' 1961 realization that on a log-log plot of crack growth rate vs stress intensity factor showed a linear relationship linear plot. Using this law, one can quantitative predictions about the residual life of a specimen given a particular crack size. Finding the beginning of the initiation of fast crack initiation: One can then find the remaining lifetime using the following simple mathematical manipulations: From here we can integrate over the size of the crack: References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Paris'_law". A list of authors is available in Wikipedia. |