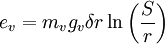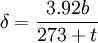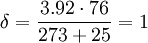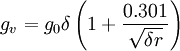My watch list

Peek's law

In physics, Peek's law is a description of the conditions necessary for corona discharge between two wires:

$e_v = m_v g_v \delta r \ln \left ({S \over r} \right )$

Additional recommended knowledge

Weighing the right way

Better weighing performance in 6 easy steps

Daily Sensitivity Test

e_v is the "visual critical corona voltage" or "corona inception voltage" (CIV), the voltage (in kilovolts) required to initiate a visible corona discharge between the wires.

m_v is an irregularity factor to account for the condition of the wires. For smooth, polished wires, m_v = 1. For roughened, dirty or weathered wires, 0.98 to 0.93, and for cables, 0.87 to 0.83.

r is the radius of the wires

S is the distance between the wires

δ is the air density factor. It is calculated by the equation:

$\delta = {3.92 b \over 273 + t}$

where

b = pressure in centimeters of mercury
t = temperature in degrees Celsius

At SATP (25°C and 76 cmHg):

$\delta = {3.92\cdot76 \over 273 + 25} = 1$

g_v is the "visual critical" potential gradient, and is calculated by the equation:

$g_v = g_0 \delta \left ( 1 + {0.301 \over \sqrt{\delta r}} \right )$

where g₀ is the "disruptive critical" potential gradient, about 30 kV/cm for air ^[1]

References

^ Hong, Alice (2000). Electric Field to Produce Spark in Air (Dielectric Breakdown). The Physics Factbook.

F.W. Peek (1929). Dielectric Phenomena in High Voltage Engineering. McGraw-Hill.
High Voltage Engineering Fundamentals, E.Kuffel and WS Zaengl, Pergamon Press, p366

Category: Plasma physics