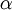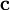To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
STO-nG basis setsProduct highlight
STO-nG basis setsSTO-nG basis sets are the minimal basis sets, where 'n' represents the number of primitive Gaussian functions comprising a single basis set. For minimal basis sets, the core and valence orbitals are represented by same number primitive Gaussian functions STO-1G basis set
STO-2G basis setIn general an STO-nG basis set is a linear combination of 'n' primitive Gaussian functions. The STO-nG basis sets are usually represented by the exponents and the corresponding coefficients. Thus an STO-2G [Ref. 1] basis set which is a linear combination of 2 primitive Gaussian functions can be represented as follows.
AccuracyThe exact energy of the 1s electron of H atom is -0.5 hartree. Following table illustrates the increase in accuracy as the number of primitive Gaussian functions increases in the basis set.
References :[1] http://gnode2.pnl.gov/bse/portal |
||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "STO-nG_basis_sets". A list of authors is available in Wikipedia. |





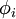 . For example, an STO-3G basis set for the 1s orbital of H atom is a linear combination of 3 primitive Gaussian functions. It is easy to calculate the energy of an electron in the 1s orbital of H atom represented by STO-nG basis sets. In the following sections, the structure of the STO-nG minimal basis sets are explained with H atom as an example.
. For example, an STO-3G basis set for the 1s orbital of H atom is a linear combination of 3 primitive Gaussian functions. It is easy to calculate the energy of an electron in the 1s orbital of H atom represented by STO-nG basis sets. In the following sections, the structure of the STO-nG minimal basis sets are explained with H atom as an example.
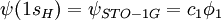 , where
, where 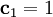 and
and
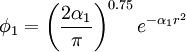 .
The optimum value of
.
The optimum value of 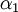 is the one which gives the minimum value for the Energy of the 1s electron of H atom. The exponent
is the one which gives the minimum value for the Energy of the 1s electron of H atom. The exponent 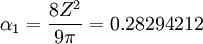 and for the value
and for the value 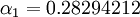 , the energy of the 1s electron of H atom can be calculated as
, the energy of the 1s electron of H atom can be calculated as 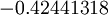 hartree. The expression for the energy of the 1s electron of H atom is a function only of
hartree. The expression for the energy of the 1s electron of H atom is a function only of 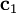 ,
, 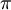 . For convenience, the basis set details can be represented as follows
. For convenience, the basis set details can be represented as follows