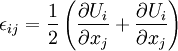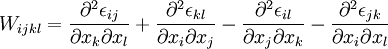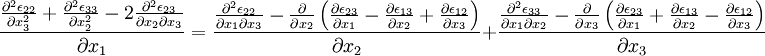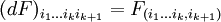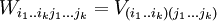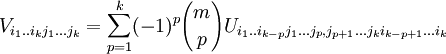Saint-Venant's compatibility condition

In the mathematical theory of elasticity the strain ε is related to a displacement field U by

Additional recommended knowledge

How to ensure accurate weighing results every day?

Better weighing performance in 6 easy steps

Correct Test Weight Handling Guide: 12 Practical Tips

Saint-Venant derived the compatibility condition for an arbitrary symmetric second rank tensor field to be of this form. The integrability condition takes the form of the vanishing of the Saint-Venants tensor^[1] defined by

Due to the symmetry conditions W_ijkl = W_klij = − W_jikl = W_ijlk there are only six (in the three dimensional case) distinct components of W. These six equations are not independent as verified by for example

and there are two further relations obtained by cyclic permutation. However, in practise the six equations are preferred. In its simplest form of course the components of ε must be assumed twice continuously differentiable, but more recent work ^[2] proves the result in a much more general case.

This can be thought of as an analogue, for symmetric tensor fields, of Poincare's lemma for skew-symmetric tensor fields (differential forms). The result can be generalized to higher rank symmetric tensor fields^[3]. Let F be a symmetric rank-k tensor field on an open set in n-dimensional Euclidean space, then the symmetric derivative is the rank k+1 tensor field defined by

where we use the classical notation that indices following a comma indicate differentiation and groups of indices enclosed in brackets indicate symmetrization over those indices. The Saint-Venant tensor W of a symmetric rank-k tensor field U is defined by

with

On a simply connected domain in Euclidean space W = 0 implies that U = dF for some rank k-1 symmetric tensor field F.

References

1. ^ N.I. Muskhelishvili, Some Basic Problems of the Mathematical Theory of Elasticity. Leyden: Noordhoff Intern. Publ., 1975.
2. ^ C Amrouche, PG Ciarlet, L Gratie, S Kesavan, On Saint Venant's compatibility conditions and Poincaré's lemma, C. R. Acad. Sci. Paris, Ser. I, 342 (2006), 887-891. doi:10.1016/j.crma.2006.03.026
3. ^ V.A. Sharafutdinov, Integral Geometry of Tensor Fields, VSP 1994,ISBN 906764165X. Chapter 2.