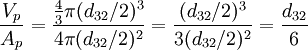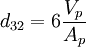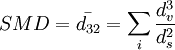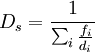To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Sauter diameter
The Sauter mean diameter (SMD) is defined as the diameter of a sphere that has the same volume/surface area ratio as a particle of interest. Originally developed by German scientist, J. Sauter in the late 1920s. The SMD is common measure in fluid dynamics as a way estimating the average particle size. Several methods have been devised to obtain a good estimate of the SMD. The SMD is typically defined in terms of the surface diameter, ds: Product highlightand volume diameter, dv: where Ap and Vp are the surface area and volume of the particle, respectively. ds and dv are usually measured directly by other means without knowledge of Ap or Vp. The Sauter diameter for a given particle is: If the actual surface area, Ap and volume, Vp of the particle are known the equation simplifies further:
The provides intrinsic data that helps determine the particle size for fluid problems. ApplicationsThe Sauter mean diameter (SMD) can be defined as the diameter of a drop having the same volume/surface area ratio as the entire spray.
Sauter Mean Diameter (SMD) is also referred to as D[3,2]. It is especially important in calculations where the active surface area is important. Such areas include catalysis and applications in fuel combustion. See also
|
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Sauter_diameter". A list of authors is available in Wikipedia. |


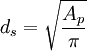



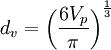
![SD = D[3,2] = d_{32} = \frac{d_v^3}{d_s^2}](images/math/5/f/5/5f58503d7101fe853b2352be47dc854c.png)