To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Spalart-Allmaras Turbulence ModelSpalart-Allmaras model is a one equation model for the turbulent viscosity. Product highlight
Original modelThe turbulent eddy viscosity is given by The rotation tensor is given by and d is the distance from the closest surface. The constants are Modifications to original modelAccording to Spalart it is safer to use the following values for the last two constants: Other models related to the S-A model: DES (1999) [1] DDES (2006) Model for compressible flowsThere are two approaches to adapting the model for compressible flows. In the first approach the turbulent dynamic viscosity is computed from where ρ is the local density. The convective terms in the equation for where the right hand side (RHS) is the same as in the original model. Boundary conditionsWalls: Freestream: Ideally This is if the trip term is used to "start up" the model. A convenient option is to set Outlet: convective outlet. References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Spalart-Allmaras_Turbulence_Model". A list of authors is available in Wikipedia. |





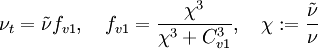
![\frac{\partial \tilde{\nu}}{\partial t} + u_j \frac{\partial \tilde{\nu}}{\partial x_j} = C_{b1} [1 - f_{t2}] \tilde{S} \tilde{\nu} + \frac{1}{\sigma} \{ \nabla \cdot [(\nu + \tilde{\nu}) \nabla \tilde{\nu}] + C_{b2} | \nabla \nu |^2 \} - \left[C_{w1} f_w - \frac{C_{b1}}{\kappa^2} f_{t2}\right] \left( \frac{\tilde{\nu}}{d} \right)^2 + f_{t1} \Delta U^2](images/math/4/7/6/476216889d1ea0604979b921eae3428c.png)
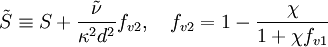
![f_w = g \left[ \frac{ 1 + C_{w3}^6 }{ g^6 + C_{w3}^6 } \right]^{1/6}, \quad g = r + C_{w2}(r^6 - r), \quad r \equiv \frac{\tilde{\nu} }{ \tilde{S} \kappa^2 d^2 }](images/math/0/9/b/09b19885ed6dffe3dec850e2516f1696.png)
![f_{t1} = C_{t1} g_t \exp\left( -C_{t2} \frac{\omega_t^2}{\Delta U^2} [ d^2 + g^2_t d^2_t] \right)](images/math/9/9/3/993b41d0ba795e0b3877d041c4cff1cb.png)
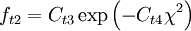
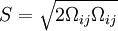
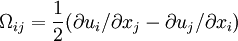
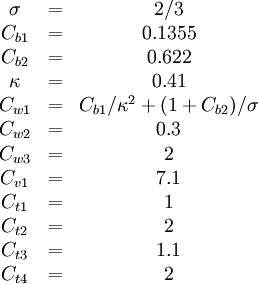
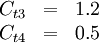
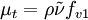
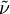 are modified to
are modified to
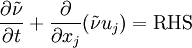
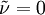
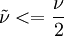 can be used.
can be used.
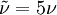 in the freestream. The model then provides "Fully Turbulent" behavior, i.e., it becomes turbulent in any region that contains shear.
in the freestream. The model then provides "Fully Turbulent" behavior, i.e., it becomes turbulent in any region that contains shear.


