Spectral element method

In mathematics, the spectral element method is a high order finite element method.

Introduced in a 1984 paper^[1] by A. T. Patera, the abstract begins: "A spectral element method that combines the generality of the finite element method with the accuracy of spectral techniques..."

The spectral element method is an elegant formulation of the finite element method with a high degree piecewise polynomial basis. The only relationship it has with the spectral method is its good convergence properties.

Additional recommended knowledge

Weighing the right way

Better weighing performance in 6 easy steps

Guide to balance cleaning: 8 simple steps

Discussion

The spectral method expands the solution in trigonometric series, a chief advantage is that the resulting method is of very high order. This approach relies on the fact that trigonometric polynomials are an orthonormal basis for L²(Ω). The spectral element method chooses instead high degree piecewise polynomial basis functions, also achieving a very high order of accuracy.

A-priori error estimate

The classic analysis of Galerkin methods and Céa's lemma holds here and it can be shown that, if u is the solution of the weak equation, u_N is the approximate solution and :

where C is independent from N and s is no larger than the degree of the piecewise polynomial basis. As we increase N, we can also increase the degree of the basis functions. In this case, if u is an analytic function:

where γ depends only on u.

Related methods

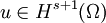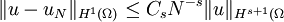
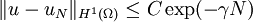
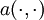• G-NI or SEM-NI: these are the most used spectral methods. The Galerkin formulation of spectral methods or spectral element methods, for G-NI or SEM-NI respectively, is modified and Gaussian numerical integration is used instead of integrals in the definition of the bilinear form and in the functional F. These method are a family of Petrov-Galerkin methods their convergence is a consequence of Strang's lemma.
• The spectral element method uses tensor product space spanned by nodal basis functions associated with Gauss-Lobatto points. In contrast, the p-version finite element method spans a space of high order polynomials by nodeless basis functions, chosen approximately orthogonal for numerical stability. Since not all interior basis functions need to be present, the p-version finite element method can create a space that that contains all polynomials up to a given degree with many fewer degrees of freedom. However, some speedup techniques possible in spectral methods due to their tensor-product character are no longer available. The name p-version means that accuracy is increased by increasing the order of the approximating polynomials (thus, p) rather than decreasing the mesh size, h. The h-p finite element method increases the order and decreases the mesh size at the same time.

Notes

1. ^ A. T. Patera. A spectral element method for fluid dynamics - Laminar flow in a channel expansion. Journal of Computational Physics, 54:468--488, 1984.