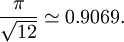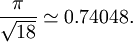Sphere packing

  In mathematics, sphere packing problems are problems concerning arrangements of non-overlapping identical spheres which fill a space. Usually the space involved is three-dimensional Euclidean space. However, sphere packing problems can be generalised to two dimensional space (where the "spheres" are circles), to n-dimensional space (where the "spheres" are hyperspheres) and to non-Euclidean spaces such as hyperbolic space.

A typical sphere packing problem is to find an arrangement in which the spheres fill as large a proportion of the space as possible. The proportion of space filled by the spheres is called the density of the arrangement. As the density of an arrangement can vary depending on the volume over which it is measured, the problem is usually to maximise the average or asymptotic density, measured over a large enough volume.

A regular arrangement (also called a periodic or lattice arrangement) is one in which the centres of the spheres form a very symmetric pattern called a lattice. Arrangements in which the spheres are not arranged in a lattice are called irregular or aperiodic arrangements. Regular arrangements are easier to handle than irregular ones—their high degree of symmetry makes it easier to classify them and to measure their densities.

Additional recommended knowledge

Safe Weighing Range Ensures Accurate Results

What is the Sensitivity of my Balance?

Daily Sensitivity Test

Circle packing

In two dimensional Euclidean space, Carl Friedrich Gauss proved that the regular arrangement of circles with the highest density is the hexagonal packing arrangement, in which the centres of the circles are arranged in a hexagonal lattice (staggered rows, like a honeycomb), and each circle is surrounded by 6 other circles. The density of this arrangement is

In 1940, Hungarian mathematician László Fejes Tóth proved that the hexagonal lattice is the densest of all possible circle packings, both regular and irregular.

The branch of mathematics generally known as "circle packing", however, is not concerned with dense packing of equal-sized circles but with the geometry and combinatorics of packings of arbitrarily-sized circles; these give rise to discrete analogs of conformal mapping, Riemann surfaces and the like.

Sphere packing

Regular packing

Main article: Close-packing

In three-dimensional Euclidean space, let us consider a plane with a compact arrangement of spheres on it. If we consider three neighbouring spheres, we can put a fourth sphere in the hollow between the three bottom spheres. If we do this "everywhere" in a second plane above the first, we create a new compact arrangement. The third layer can superimpose to the first one, or the spheres can be upon a hollow of the first layer. There are thus three types of planes, called A, B and C.

Gauss proved these arrangements have the highest density amongst the regular arrangements.

The two most common arrangements are called cubic close packing (or face centred cubic) — ABCABC… alternance — and hexagonal close packing — ABAB… alternance. But all combinations are possible (ABAC, ABCBA, ABCBAC, etc.). In all of these arrangements each sphere is surrounded by 12 other spheres, and both arrangements have an average density of

In 1611 Johannes Kepler had conjectured that this is the maximum possible density for both regular and irregular arrangements — this became known as the Kepler conjecture. In 1998 Thomas Hales, following the approach suggested by László Fejes Tóth in 1953, announced the proof of the Kepler conjecture. Hales' proof is a proof by exhaustion involving checking of many individual cases using complex computer calculations. Referees have said that they are "99% certain" of the correctness of Hales' proof, so the Kepler conjecture has almost certainly been proved.

Irregular packing

Main article: Random close pack

If we attempt to build a densely packed collection of spheres, we will be tempted to always place the next sphere in a hollow between three packed spheres. If five spheres are assembled in this way, they will be consistent with one of the regularly packed arrangements described above. However, the sixth sphere placed in this way will render the structure inconsistent with any regular arrangement. (Chaikin, 2007). This results in the possibility of a random close packing of spheres which is stable against compression.

When spheres are randomly added to a container and then compressed, they will generally form what is known as an "irregular" or "jammed" packing configuration when they can be compressed no more. This irregular packing will generally have a density of about 64% of the density of the spheres themselves. This situation is unlike the case of one or two dimensions, where compressing a collection of 1-dimensional or 2-dimensional spheres (i.e. line segments or disks) will yield a regular packing.

Hypersphere packing

In dimensions higher than three, the densest regular packings of hyperspheres are known up to 8 dimensions. Very little is known about irregular hypersphere packings — it is possible that in some dimensions the densest packing may be irregular. Some support for this conjecture comes from the fact that in certain dimensions (e.g. 10) the densest known irregular packing is better than the densest known regular packing.

Dimension 24 is special due to the existence of the Leech lattice, which has the best kissing number and for a long time was suspected to be the densest lattice packing. In 2004, Cohn and Kumar¹ published a preprint proving this conjecture, and in addition showing that an irregular packing may improve over the Leech lattice packing, if at all, by no more than 2×10^-30.

Another line of research in high dimensions is trying to find asymptotic bounds for the density of the densest packings. Currently the best known result is that there exists a lattice in dimension n with density bigger or equal to cn2 ^{− n} for some number c.

Hyperbolic space

Although the concept of circles and spheres can be extended to hyperbolic space, finding the densest packing becomes much more difficult. In a hyperbolic space there is no limit to the number of spheres that can surround another sphere (for example, Ford circles can be thought of as an arrangement of identical hyperbolic circles in which each circle is surrounded by an infinite number of other circles). The concept of average density also becomes much more difficult to define accurately.

Despite these difficulties, Charles Radin and Lewis Bowen of the University of Texas at Austin showed in May 2002 that the densest packings in any hyperbolic space are almost always irregular.

Other spaces

Sphere packing on the corners of a hypercube (with the spheres defined by Hamming distance) corresponds to designing error-correcting codes: if the spheres have radius d, then their centers are codewords of a d-error-correcting code. Lattice packings correspond to linear codes. There are other, subtler relationships between Euclidean sphere packing and error-correcting codes; thus, the binary Golay code is closely related to the 24-dimensional Leech lattice.

See also

• Kissing number problem
• Sphere-packing bound

References

• Conway, J.H. & Sloane, N.J.H. (1998) "Sphere Packings, Lattices and Groups" (Third Edition). ISBN 0-387-98585-9
• Lewis Bowen & Charles Radin (2003) "Densest Packings of Equal Spheres in Hyperbolic Space" (pre-print of article in Discrete & Computational Geometry)
• N. J. A. Sloane, The Sphere Packing Problem, arXiv:math.CO/0207256 (A technical survey from 2002).
• C. A. Rogers, Existence Theorems in the Geometry of Numbers, The Annals of Mathematics, 2nd Ser., 48:4 (1947), 994-1002 (The n2 ^{− n} result mentioned above. Despite 60 years of research, only the constant was improved in this result).
• Henry Cohn and Abhinav Kumar, The densest lattice in twenty-four dimensions, arXiv:math.MG/0403263(The solution for the 24 dimensional case).
• T. Aste and D. Weaire "The Pursuit of Perfect Packing" (Institute Of Physics Publishing London 2000) ISBN 0-7503-0648-3
• Chaikin, Paul "Reference Frame", Physics Today, June 2007 p8.

In popular culture

• Kurt Vonnegut Jr.'s novel, Cat's Cradle, mentions a chemical Ice 9 which is made based on the principles of being able to stack cannon balls in different ways. Ice 9 is a fictional H₂O molecule that is stacked in a certain way which makes it turn any water it touches into Ice 9.

• "Circle Packing" (Wolfram MathWorld)
• "Kugelpackungen (Sphere Packing)" (T.E. Dorozinski)