To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Taylor coneA Taylor cone refers to the cone observed in electrospray and hydrodynamic spray processes from which a jet of charged particles emanates above a threshold voltage. Aside from electrospray ionization in mass spectrometry the Taylor cone is important in colloid thrusters used in fine control and high efficiency (low power) thrust of spacecraft. Product highlight
HistoryThis cone was described by Sir Geoffrey Ingram Taylor in 1964 before electrospray was "discovered".[1] This work followed on the work of Zeleny[2] where in 1917 he photographed a cone-jet of glycerine under high electric field and the work of several others, Wilson & Taylor (1925),[3] Nolan (1926)[4] and Macky (1931).[5] Taylor was primarily interested in the behavior of water droplets in strong electric fields, such as in thunderstorms. Taylor cone formationWhen a small volume of electrically conductive liquid is exposed to an electric field the shape of liquid starts to deform from the shape caused by surface tension alone. As the voltage is increased the effect of the electric field becomes more prominent and as it approaches exerting a similar amount of force on the droplet as the surface tension does a cone shape begins to form with convex sides and a rounded tip. This approaches the shape of a straight generatrix (cone) with a whole angle (width) of 98.6°. When a certain threshold voltage has been reached the slightly rounded tip inverts and emits a jet of liquid. This is called a cone-jet and is the beginning of the electrospray process in which ions may be transferred to the gas phase. It is generally found that in order to achieve a stable cone-jet a slightly higher than threshold voltage must be used. As the voltage is increased even more other modes of droplet disintegration are found. The term Taylor cone can specifically refer to the theoretical limit of a perfect cone of exactly the predicted angle or generally refer to the approximately conical portion of a cone-jet after the electrospray process has begun. TheorySir Geoffrey Ingram Taylor in 1964 described this phenomenon, theoretically derived based on general assumptions that the requirements to form a perfect cone under such conditions required a semi-vertical angle of 49.3° (a whole angle of 98.6°) and demonstrated that the shape of such a cone approached the theoretical shape just before jet formation. This angle is known as the Taylor angle. This angle is more precisely Taylor's derivation is based on two assumptions: (1) that the surface of the cone is an equipotential surface and (2) that the cone exists in a steady state equilibrium. To meet both of these criteria the electric field must have azimuthal symmetry and have where References
External links |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Taylor_cone". A list of authors is available in Wikipedia. |





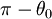 where
where 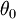 is the first zero of
is the first zero of 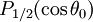 (the Legendre polynomial of order 1/2).
(the Legendre polynomial of order 1/2).
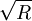 dependence to counter the surface tension to produce the cone. The solution to this problem is:
dependence to counter the surface tension to produce the cone. The solution to this problem is:
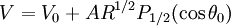
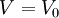 (equipotential surface) exists at a value of
(equipotential surface) exists at a value of 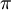 which there is only one at 130.7099°. The complement of this angle is the Taylor angle.
which there is only one at 130.7099°. The complement of this angle is the Taylor angle.


