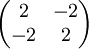Toda field theory

In the study of field theory and partial differential equations, a Toda field theory is derived from the following Lagrangian:

Additional recommended knowledge

Recognize and detect the effects of electrostatic charges on your balance

Safe Weighing Range Ensures Accurate Results

Don't let static charges disrupt your weighing accuracy

Here x and t are spacetime coordinates, (,) is the Killing form of a real r-dimensional Cartan algebra of a Kac-Moody algebra over , α_i is the i^th simple root in some root basis, n_i is the Coxeter number, m is the mass (or bare mass in the quantum field theory version) and β is the coupling constant.

Then a Toda field theory is the study of a function φ mapping 2 dimensional Minkowski space satisfying the corresponding Euler-Lagrange equations.

If the Kac-Moody algebra is finite, it's called a Toda field theory. If it is affine, it is called an affine Toda field theory (after the component of φ which decouples is removed) and if it is hyperbolic, it is called a hyperbolic Toda field theory.

Toda field theories are integrable models and their solutions describe solitons.

The sinh-Gordon model is the affine Toda field theory with the generalized Cartan matrix

and a positive value for β after we project out a component of φ which decouples.

The sine-Gordon model is the model with the same Cartan matrix but an imaginary β.

References

• affine toda on arxiv.org