Van 't Hoff factor

In physical chemistry, the van 't Hoff factor i is the number of moles of solute actually in solution per mole of solid solute added. Equivalently, i refers to the ratio of true molecular mass to calculated molecular methods by colligative methods. It is named after Jacobus Henricus van 't Hoff, the winner of the first Nobel Prize in chemistry.

The van 't Hoff factor is important in quantitative analysis of colligative properties, such as vapor pressure and freezing point depression.

Additional recommended knowledge

Better weighing performance in 6 easy steps

Weighing the right way

Essential Laboratory Skills Guide

Physical significance of i

In NaCl for example, i = 2 indicates that by using the colligative properties equations without the i factor, we're actually calculating the molar mass of each of the Na⁺ and Cl^- ions in solution. The molar mass of NaCl should be twice that number because it originally dissociated to produce one Na⁺ ion and one Cl^- ion per formula unit of NaCl; the sum of the masses of the two ions should yield the mass of one formula unit of NaCl. Note that even if the mass of Na⁺ and Cl^- weren't equal (which is the case), we're only calculating the average mass of the two particles using our colligative properties analysis. Hence multiplying that average number by two, we would be calculating the molar mass of NaCl.

• When solute particles associate in solution, i is less than unity. [Eg. Ethanoic acid in benzene, benzoic acid in benzene]
• When solute particles dissociate in solution, i is greater than unity. [Eg. Sodium chloride in water, potassium chloride in water, magnesium chloride in water]
• When solute particles neither dissociate nor associate in solution, i equals unity. [Eg. Glucose in water]

Relation to degree of dissociation

• When a solute dissociates in solution,

• When a solute associates in solution,

Where α is the degree of association/ dissociation and n is the number of particles produced during association or dissociation per molecule or formula unit of the solute.

Illustrative examples

• For NaCl in water, which dissociates completely into Na⁺ and Cl^- ions in solution, α equals 1 (100%) and n equals two (since two ions, namely one Na⁺ ion and one Cl^- ion are produced in solution per formula unit of NaCl). van't Hoff factor for NaCl is then calculated as two which means that the true formula weight of NaCl is twice that calculated by colligative methods ignoring the van't Hoff factor.
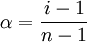
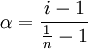
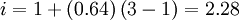• For a sulfuric acid (H₂SO₄) solution, in which 64% of the molecules are ionized, i could be calculated by , as each molecule results in one sulfate ion and two hydronium ions. That same result could be achieved by realizing that, for each 100 molecules of acid, 36 are kept and 64 are ionized, resulting in 192 ions and 36 molecules, adding up to a total of 228 particles. Therefore, there would be 2.28 times as many ions as there were acid molecules before.

See also

• Colligative properties
• Solutions
• Raoult's law