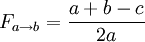To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
View factorIn Radiative heat transfer, a view factor In a complex 'scene' there can be any number of different objects, which can be divided in turn in to even more surfaces and surface segments. View factors are also sometimes known as configuration factors, form factors or shape factors. Product highlight
Summation of view factorsBecause all of the radiation leaving a surface is a fixed amount, one can add up all of the view factors from a given surface Si, and they will always add up to one:
For example, consider a case where two blobs, 'A' and 'B' are floating around in a cavity 'C'. All the radiation that leaves surface A must either hit surface B or the cavity surface C, or if the surface A is concave, might again hit A. In terms of fractions, 100% of the radiation leaving surface A is divided up between surfaces A, B, and C, which is equivalent to the expression above. Confusion often arises when considering the radiation that arrives at a target surface. In that case there, summation of view factors does not apply, because each 'incoming' view factor is a fraction of the radiation leaving some other surface: there is no reason for those fractions to add up to anything at all; in fact they can add up to less than one, or many times one, but this value has no significance. Self-viewing surfacesFor a convex surface, no radiation can leave the surface and then hit it later, because radiation travels in straight lines. Hence, for convex surfaces, For concave surfaces, this doesn't apply, and so for concave surfaces ReciprocityThe reciprocity theorem for view factors allows one to calculate
View factors in a triangleFor a triangle with sides of length a, b and c, the view factor
Hottel's Crossed String RuleThe crossed string rule allows calculation of radiation transfer between opposite sides of a quadrilateral, and furthermore applies in some cases where there is partial obstruction between the objects. For a derivation and further details, see this article by G H Derrick. See alsoA large number of 'standard' view factors can be calculated with the use of tables that are commonly provided in heat transfer textbooks.
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "View_factor". A list of authors is available in Wikipedia. |


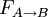 is the proportion of all that radiation which leaves surface
is the proportion of all that radiation which leaves surface 


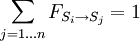
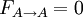
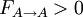
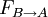 if one already knows
if one already knows 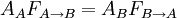
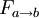 is given by
is given by