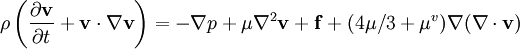Volume viscosity

Volume viscosity (also called bulk viscosity) appears in the Navier-Stokes equation if it is written for compressible fluid, as described in the most books on general hydrodynamics ^[1], ^[2], and the acoustics ^[3],^[4].

Additional recommended knowledge

Better weighing performance in 6 easy steps

What is the Sensitivity of my Balance?

How to quickly check pipettes?

where μ^v is second viscosity coefficient. Authors who use the alternative term bulk viscosity for the same parameter include ^[5], ^[6]. This additional term disappears for incompressible fluid, when the divergence of the flow equals 0.

This viscosity parameter is additional to the usual dynamic viscosity μ. The volume viscosity becomes important only for such effects where fluid compressibility is essential. Examples would include shock waves and sound propagation. It appears in the Stokes' law (sound attenuation) that describes propagation of sound in Newtonian liquid.

The volume viscosity of many fluids is inaccurately known, despite its fundamental role for fluid dynamics at high frequencies. The only values for the volume viscosity of simple Newtonian liquids known to us come from the old Litovitz and Davis review, see References. They report the volume viscosity of water at 15 C⁰ is 3.09 centipoise

Modern Acoustic rheometers are able to measure this parameter, see External links.

References

1. ^ Happel, J. and Brenner , H. "Low Reynolds number hydrodynamics", Prentice-Hall, (1965)
2. ^ Landau, L.D. and Lifshitz, E.M. "Fluid mechanics", Pergamon Press,(1959)
3. ^ Litovitz, T.A. and Davis, C.M. In "Physical Acoustics", Ed. W.P.Mason, vol. 2, chapter 5, Academic Press, NY, (1964)
4. ^ Dukhin, A.S. and Goetz, P.J. "Ultrasound for characterizing colloids", Elsevier, (2002)
5. ^ Morse, P.M. and Ingard, K.U. "Theoretical Acoustics", Princeton University Press(1986)
6. ^ Graves, R.E. and Agrow, B.M. "Bulk viscosity:Past to Present", J. of Thermodynamics and Heat Transfer,13, 3, 337-342 (1999)

Category