To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Wien's displacement law
where
The two digits between the parentheses denotes the uncertainty (the standard deviation at 68.27% confidence level) in the two least significant digits of the mantissa. For optical wavelengths, it is often more convenient to use the nanometer in place of the meter as the unit of measure. In this case… Product highlight
Explanation and familiar approximate applicationsThe law is named for Wilhelm Wien, who formulated the relationship in 1893 based on a thermodynamic argument. Wien considered adiabatic expansion of a cavity containing waves of light in thermal equilibrium. He showed that under adiabatic expansion or contraction, the energy of light changes in the exact same way as the frequency. This means that the peak frequency should change with temperature as the energy goes. Wien did not interpret his constant b as a new fundamental constant of nature. This was done by Planck. Wien's displacement law states that the hotter an object is, the shorter the wavelength at which it will emit most of its radiation, and further that the frequency for maximal or peak radiation power is found by dividing Wien's constant by the temperature in kelvins. Examples:
[See for example the article color, because of the spread resulting in white light. Due to the Rayleigh scattering of blue light by the atmosphere this white light is separated somewhat, resulting in a blue sky and a yellow sun]. Wien's constant may be used in different units, and many examples to calculate familiar situation types of radiation required use of only one or two significant figures:
Frequency formIn terms of frequency f (in hertz), Wien's displacement law becomes where
Because the spectrum resulting from Planck's law of black body radiation takes a different shape in the frequency domain from that of the wavelength domain, the frequency location of the peak emission does not correspond to the peak wavelength using the simple relationship between frequency, wavelength, and the speed of light. DerivationWilhelm Wien first derived this law in 1893 by applying the laws of thermodynamics to electromagnetic radiation[1]. As is typically the case with thermodynamic arguments, Wien's derivation determines the functional form of the relationship but does not specify the values of the constants b (in the temperature form) or α (in the frequency form.) A modern variant of Wien's derivation can be found in the textbook by Wannier [2]. Today, the usual practice is to derive the relationship from Planck's law of black body radiation, as this procedure also yields expressions for the constants b and α in terms of fundamental constants. From Planck's law, we know that the spectrum of black body radiation is The value of λ for which this function is maximized is sought. To find it, we differentiate u(λ,T) with respect to λ and set it equal to zero If we define then This equation cannot be solved in terms of elementary functions. It can be solved in terms of Lambert's Product Log function but an exact solution is not important in this derivation. One can easily find the numerical value of x
Solving for the wavelength λ in units of nanometers, and using units of kelvins for the temperature yields:
The frequency form of Wien's displacement law is derived using similar methods, but starting with Planck's law in terms of frequency instead of wavelength. References and notes
Categories: Statistical mechanics | Foundational quantum physics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Wien's_displacement_law". A list of authors is available in Wikipedia. |


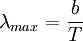
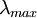 is the peak wavelength in
is the peak wavelength in 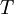 is the temperature of the blackbody in
is the temperature of the blackbody in 


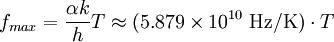
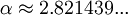 is a constant resulting from the numerical solution of the maximization equation,
is a constant resulting from the numerical solution of the maximization equation,
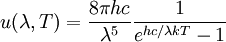
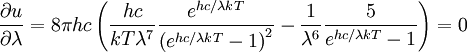
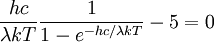
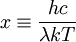
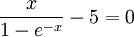
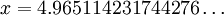 (dimensionless)
(dimensionless)
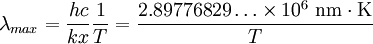 .
.


