To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Gaussian beamIn optics, a Gaussian beam is a beam of electromagnetic radiation whose transverse electric field and intensity (irradiance) distributions are described by Gaussian functions. Many lasers emit beams with a Gaussian profile, in which case the laser is said to be operating on the fundamental transverse mode, or "TEM00 mode" of the laser's optical resonator. When refracted by a lens, a Gaussian beam is transformed into another Gaussian beam (characterized by a different set of parameters), which explains why it is a convenient, widespread model in laser optics. The mathematical function that describes the Gaussian beam is a solution to the paraxial form of the Helmholtz equation. The solution, in the form of a Gaussian function, represents the complex amplitude of the electric field, which propagates along with the corresponding magnetic field as an electromagnetic wave in the beam. Product highlight
Mathematical formFor a Gaussian beam, the complex electric field amplitude, measured in volts per meter, at a distance r from its centre, and a distance z from its waist, is given by where
The functions w(z), R(z), and ζ(z) are parameters of the beam, which we define below. The corresponding time-averaged intensity (or irradiance) distribution, measured in watts per square meter, is where w(z) is the radius at which the field amplitude and intensity drop to 1/e and 1/e2, respectively. This parameter is called the beam radius or spot size of the beam. E0 and I0 are, respectively, the electric field amplitude and intensity at the center of the beam at its waist, that is E0 = | E(0,0) | and
I0 = I(0,0). The constant Beam parametersThe geometry and behavior of a Gaussian beam are governed by a set of beam parameters, which are defined in the following sections. Beam width or "spot size"For a Gaussian beam propagating in free space, the spot size w(z) will be at a minimum value w0 at one place along the beam axis, known as the beam waist. For a beam of wavelength λ at a distance z along the beam from the beam waist, the variation of the spot size is given by where the origin of the z-axis is defined, without loss of generality, to coincide with the beam waist, and where is called the Rayleigh range. Rayleigh range and confocal parameterAt a distance from the waist equal to the Rayleigh range z0, the width w of the beam is The distance between these two points is called the confocal parameter or depth of focus of the beam: Radius of curvatureR(z) is the radius of curvature of the wavefronts comprising the beam. Its value as a function of position is Beam divergenceThe parameter w(z) approaches a straight line for The total angular spread of the beam far from the waist is then given by Because of this property, a Gaussian laser beam that is focused to a small spot spreads out rapidly as it propagates away from that spot. To keep a laser beam very well collimated, it must have a large diameter. Since the gaussian beam model uses the paraxial approximation, it fails when wavefronts are tilted by more than about 30° from the direction of propagation[1]. From the above expression for divergence, this means the Gaussian beam model is valid only for beams with waists larger than about 2λ/π. Laser beam quality is quantified by the beam parameter product (BPP). For a Gaussian beam, the BPP is the product of the beam's divergence and waist size w0. The BPP of a real beam is obtained by measuring the beam's minimum diameter and far-field divergence, and taking their product. The ratio of the BPP of the real beam to that of an ideal Gaussian beam at the same wavelength is known as M² ("M squared"). The M² for a Gaussian beam is one. All real laser beams have M² values greater than one, although very high quality beams can have values very close to one. Gouy phaseThe longitudinal phase delay or Gouy phase of the beam is Complex beam parameterThe complex beam parameter is It is often convenient to calculate this quantity in terms of its reciprocal: The complex beam parameter plays a key role in the analysis of gaussian beam propagation, and especially in the analysis of optical resonator cavities using ray transfer matrices. Power and intensityPower through an apertureThe power P (in watts) passing through a circle of radius r in the transverse plane at position z is where is the total power transmitted by the beam. For a circle of radius Similarly, about 95 percent of the beam's power will flow through a circle of radius Peak and average intensityThe peak intensity at an axial distance z from the beam waist is calculated using L'Hôpital's rule as the limit of the enclosed power within a circle of radius r, divided by the area of the circle πr2: The peak intensity is thus exactly twice the average intensity, obtained by dividing the total power by the area within the radius w(z). See also
Notes
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Gaussian_beam". A list of authors is available in Wikipedia. |





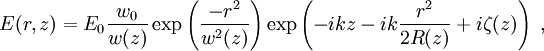
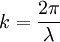 is the wave number (in
is the wave number (in 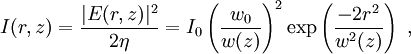
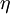 is the characteristic impedance of the medium in which the beam is propagating. For free space,
is the characteristic impedance of the medium in which the beam is propagating. For free space, 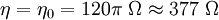 .
.
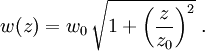
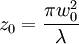
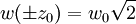
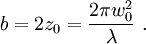
![R(z) = z \left[{ 1+ {\left( \frac{z_0}{z} \right)}^2 } \right] \ .](images/math/2/b/5/2b538c79cf44abafe7271702b9293ea1.png)
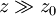 . The angle between this straight line and the central axis of the beam is called the divergence of the beam. It is given by
. The angle between this straight line and the central axis of the beam is called the divergence of the beam. It is given by
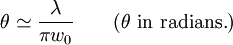
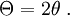
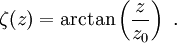
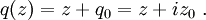
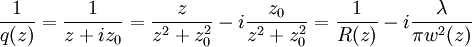
![P(r,z) = P_0 \left[ 1 - e^{-2r^2 / w^2(z)} \right]\ ,](images/math/2/5/7/2579d41377cd504505c521d40bb4a201.png)
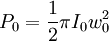
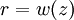 , the fraction of power transmitted through the circle is
, the fraction of power transmitted through the circle is
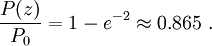
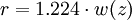 .
.
![I(0,z) =\lim_{r\to 0} \frac {P_0 \left[ 1 - e^{-2r^2 / w^2(z)} \right]} {\pi r^2} = \frac{P_0}{\pi} \lim_{r\to 0} \frac { \left[ -(-2)(2r) e^{-2r^2 / w^2(z)} \right]} {w^2(z)(2r)} = {2P_0 \over \pi w^2(z)}.](images/math/b/0/4/b04fe4abc878b8ca997a6387281f9b8b.png)


