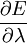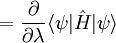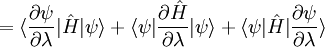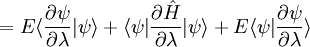To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Hellmann–Feynman theoremThe Hellmann–Feynman theorem states that once the spatial distribution of the charged particles (usually the electron clouds) has been determined by solving the Schrödinger equation, all the forces in the system can be calculated using the classical electrostatics. It is named for its independent provers Hans Hellmann (1936) and Richard Feynman (1939). Product highlightThis quantum mechanics theorem relates the energy eigenvalues of a time-independent Hamiltonian operator to the parameters composing it. In general, the theorem states that, where En is the nth Hamiltonian eigenvalue, ψn is the nth Hamiltonian eigenvector, λ is a continuous parameter of interest, and dτ implies an integration over the complete domain of the eigenvectors. The proofUsing the Dirac's bra-ket notation, we can write Note that the last step is only valid for the exact wave function, not (necessarily) for approximate ones. Hence, for instance, the Hellmann-Feynman force of a Hartree-Fock wave function differs quite significantly from the true energy gradient. See also
|
||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Hellmann–Feynman_theorem". A list of authors is available in Wikipedia. |





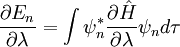
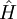 is the parameterized Hamiltonian operator,
is the parameterized Hamiltonian operator,