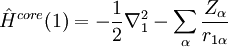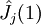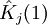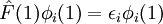To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Hartree-FockIn computational physics and computational chemistry, the Hartree-Fock (HF) method is an approximate method for the determination of the ground-state wavefunction and ground-state energy of a quantum many-body system. The Hartree-Fock method assumes that the exact, N-body wavefunction of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of N spin-orbitals. Invoking the variational principle one can derive a set of N coupled equations for the N spin-orbitals. Solution of these equations yields the Hartree-Fock wavefunction and energy of the system, which are approximations of the exact ones. The Hartree-Fock method finds its typical application in the solution of the electronic Schrödinger equation of atoms, molecules and solids but it has also found widespread use in nuclear physics. See Hartree-Fock-Bogolyubov for a discussion of its application in nuclear structure theory. The rest of this article will focus on applications in electronic structure theory. The Hartree-Fock method is also called, especially in the older literature, the self-consistent field method (SCF). The solutions to the resulting non-linear equations behave as if each particle is subjected to the mean field created by all other particles (see the Fock operator below). The equations are almost universally solved by means of an iterative, fixed-point type algorithm (see the following section for more details). This solution scheme is not the only one possible and is not an essential feature of the Hartree-Fock method. For molecules, Hartree-Fock is the central method for all ab initio quantum chemistry methods. The discussion here is only for the Restricted Hartree-Fock method, where the atom or molecule is a closed-shell system with all orbitals (atomic or molecular) are doubly occupied. Open shell systems, where some of the electrons are not paired, can be dealt with by one of two Hartree-Fock methods:
Product highlight
Brief historyThe origin of the Hartree-Fock method dates back to the end of the 1920s, soon after the derivation of the Schrödinger equation in 1926. In 1927 D.R. Hartree introduced a procedure, which he called the self consistent field method, to calculate approximate wavefunctions and energies for atoms and ions. Hartree was guided by some earlier, semi-empirical methods of the early 1920s (by E. Fues, R.B. Lindsay and himself) set in the old quantum theory of Bohr. In the Bohr model of the atom, the energy of a state with principal quantum number n is given in atomic units as E = − 1 / n2. It was observed from atomic spectra that the energy levels of many-electron atoms were well-described by applying a modified version of Bohr's formula. By introducing the quantum defect d as an empirical parameter, the energy levels of a generic atom was well approximated by the formula E = − 1 / (n + d)2, in the sense that one could reproduce fairly well the observed transitions levels observed in the X-ray region. The existence of a non-zero quantum defect was attributed to electron-electron repulsion which clearly does not exist in the isolated hydrogen atom. This repulsion resulted in partial screening of the bare nuclear charge. These early researchers later introduced other potentials containing additional empirical parameters with the hope of better reproducing the experimental data. Hartree sought to do away with empirical parameters and solve the many-body time-independent Schrödinger equation from fundamental physical principles, i.e. ab initio. His first proposed method of solution became known as the Hartree method. However, many of Hartree's contemporaries did not understand the physical reasoning behind the Hartree method: it appeared to many people to contain empirical elements, and its connection to the solution of the many-body Schrödinger equation was unclear. However, in 1928 J.C. Slater and J.A. Gaunt independently showed that Hartree's method could be couched on a sounder theoretical basis by applying the variational principle to an ansatz (trial wavefunction) as a product of single-particle functions. In 1930 Slater and V.A. Fock independently pointed out that the Hartree method did not respect the principle of antisymmetry of the wavefunction. Hartree's method used the Pauli exclusion principle in its older formulation, forbidding the presence of two electrons in the same quantum state. However, this was shown to be fundamentally incomplete in its neglect of quantum statistics. It was then shown that a Slater determinant, a determinant of one-particle orbitals first used by Heisenberg and Dirac in 1926, trivially satisfies the antisymmetric property of the exact solution and hence is a suitable ansatz for applying the variational principle. The original Hartree method can then be viewed as an approximation to the Hartree-Fock method by neglecting exchange. Fock's original method relied heavily on group theory and was too abstract for contemporary physicists to understand and implement. In 1935 Hartree reformulated the method more suitably for the purposes of calculation. The Hartree-Fock method, despite its physically more accurate picture, was little used until the advent of electronic computers in the 1950s due to the much greater computational demands over the early Hartree method and empirical models. Initially, both the Hartree method and the Hartree-Fock method were applied exclusively to atoms, where the spherical symmetry of the system allowed one to greatly simplify the problem. These approximate methods were (and are) often used together with the central field approximation, to impose that electrons in the same shell have the same radial part, and restricting the variational solution to be a spin eigenfunction. Even so, solution by hand of the Hartree-Fock equations for a medium sized atom were laborious; small molecules required computational resources far beyond what was available before 1950. Hartree-Fock algorithmThe Hartree-Fock method is typically used to solve the time-independent Schrödinger equation for a multi-electron atom or molecule as described in the Born-Oppenheimer approximation. Since there are no known solutions for many-electron systems (hydrogenic atoms and the diatomic hydrogen cation being notable one-electron exceptions), the problem is solved numerically. Due to the nonlinearities introduced by the Hartree-Fock approximation, the equations are solved using a nonlinear method such as iteration, which gives rise to the name "self-consistent field method". ApproximationThe Hartree-Fock method makes five major simplifications in order to deal with this task:
Relaxation of the last two approximations give rise to many so-called post-Hartree-Fock methods.
Variational Optimization of OrbitalsThe variational theorem states that for a time-independent Hamiltonian operator, any trial wavefunction will have an energy expectation value that is greater than or equal to the true ground state wavefunction corresponding to the given Hamiltonian. Because of this, the Hartree-Fock energy is an upper bound to the true ground state energy of a given molecule. In the context of the Hartree-Fock method, the best possible solution is at the Hartree-Fock limit, i.e. the limit of the Hartree-Fock energy as the basis set approaches completeness. (The other is the full-CI limit, where the last two approximations of the Hartree-Fock theory as described above are completely undone. It is only when both limits are attained that the exact solution is obtained.) In that case, the Hartree-Fock energy is the minimal energy over the set of Slater determinants. The starting point for the Hartree-Fock method is a set of approximate one-electron wavefunctions known as orbitals. For an atomic calculation, these are typically the orbitals for a hydrogenic atom (an atom with only one electron, but the appropriate nuclear charge). For a molecular or crystalline calculation, the initial approximate one-electron wavefunctions are typically a linear combination of atomic orbitals (LCAO). The orbitals above only account for the presence of other electrons in an average manner. In the Hartree-Fock method, the effect of other electrons are accounted for in a mean-field theory context. The orbitals are optimized by requiring them to minimize the energy of the respective Slater determinant. The resultant variational conditions on the orbitals lead to a new one-electron operator, the Fock operator. At the minimum, the occupied orbitals are eigensolutions to the Fock operator via a unitary transformation between themselves. The Fock operator is an effective one-electron Hamiltonian operator being the sum of two terms. The first is a sum of kinetic energy operators for each electron, the internuclear repulsion energy, and a sum of nuclear-electronic coulombic attraction terms. The second are Coulombic repulsion terms between electrons in a mean-field theory description; a net repulsion energy for each electron in the system, which is calculated by treating all of the other electrons within the molecule as a smooth distribution of negative charge. This is the major simplification inherent in the Hartree-Fock method, and is equivalent to the fifth simplification in the above list. Since the Fock operator depends on the orbitals used to construct the corresponding Fock matrix, the eigenfunctions of the Fock operator are in turn new orbitals which can be used to construct a new Fock operator. In this way, the Hartree-Fock orbitals are optimized iteratively until the change in total electronic energy falls below a predefined threshold. In this way, a set of self-consistent one-electron orbitals are calculated. The Hartree-Fock electronic wavefunction is then the Slater determinant constructed out of these orbitals. Following the basic postulated of quantum mechanics, the Hartree-Fock wavefunction can then be used to compute any desired chemical or physical property within the framework of the Hartree-Fock method and the approximations employed. Mathematical formulationThe Fock operatorBecause the electron-electron repulsion term of the electronic molecular Hamiltonian involves the coordinates of two different electrons, it is necessary to reformulate it in an approximate way. Under this approximation, (outlined under Hartree-Fock algorithm), all of the terms of the exact Hamiltonian except the nuclear-nuclear repulsion term are re-expressed as the sum of one-electron operators outlined below. The "(1)" following each operator symbol simply indicates that the operator is 1-electron in nature. where: is the one-electron Fock operator generated by the orbitals φj , is the one-electron core Hamiltonian, is the Coulomb operator, defining the electron-electron repulsion energy due to the orbital of the j-th electron, is the exchange operator, defining the electron exchange energy. Finding the Hartree-Fock one-electron wavefunctions is now equivalent to solving the eigenfunction equation:
where φi(1) are a set of one-electron wavefunctions, called the Hartree-Fock Molecular Orbitals. Linear combination of atomic orbitals
Typically, in modern Hartree-Fock calculations, the one-electron wavefunctions are approximated by a Linear combination of atomic orbitals. These atomic orbitals are called Slater-type orbitals. Furthermore, it is very common for the "atomic orbitals" in use to actually be composed of a linear combination of one or more Gaussian-type orbitals, rather than Slater-type orbitals, in the interests of saving large amounts of computation time. Various basis sets are used in practice, most of which are composed of Gaussian functions. In some applications, an orthogonalization method such as the Gram-Schmidt process is performed in order to produce a set of orthogonal basis functions. This can in principle save computational time when the computer is solving the Roothaan-Hall equations by converting the overlap matrix effectively to an identity matrix. However in most modern computer programs for molecular Hartree-Fock calculations this procedure is not followed due to the high numerical cost of orthogonalization and the advent of more efficient, often sparse, algorithms for solving the generalized eigenvalue problem, of which the Roothan-Hall equations are an example. Numerical stabilityNumerical stability can be a problem with this procedure and there are various ways of combating this instability. One of the most basic and generally applicable is called F-mixing or damping. With F-mixing, once a single electron wavefunction is calculated it is not used directly. Instead, some combination of that calculated wavefunction and the previous wavefunctions for that electron is used - the most common being a simple linear combination of the calculated and immediately preceding wavefunction. A clever dodge, employed by Hartree, for atomic calculations was to increase the nuclear charge, thus pulling all the electrons closer together. As the system stabilised, this was gradually reduced to the correct charge. In molecular calculations a similar approach is sometimes used by first calculating the wavefunction for a positive ion and then to use these orbitals as the starting point for the neutral molecule. Modern molecular Hartree-Fock computer programs use a variety of methods to ensure convergence of the Roothaan-Hall equations. Weaknesses, extensions, and alternativesOf the five simplifications outlined under Hartree-Fock algorithm, the fifth is typically the most important. Neglecting electron correlation can lead to large deviations from experimental results. A number of approaches to this weakness, collectively called post-Hartree-Fock methods, have been devised to include electron correlation to the multi-electron wave function. One of these approaches, Møller-Plesset perturbation theory, treats correlation as a perturbation of the Fock operator. Others expand the true multi-electron wavefunction in terms of a linear combination of Slater determinants - such as Multi-configurational self-consistent field, Configuration interaction, Quadratic configuration interaction, Complete active space SCF (CASSCF). Still others modify the Hartree-Fock wave function by multiplying it by a correlation function ("Jastrow" factor), a term which is explicitly a function of multiple electrons that cannot be decomposed into independent single-particle functions. An alternative to Hartree-Fock calculations used in some cases is density functional theory, which gives approximate solutions to both exchange and correlation energies, but is not a purely ab initio method in practice. Indeed, it is common to use calculations that are a hybrid of the two methods - the popular B3LYP schema is one such hybrid functional method. Software packagesFor a list of software packages known to handle Hartree-Fock calculations, see the Software packages section of Computational Chemistry. References
See alsoRelated fields
Concepts
People
Categories: Computational chemistry | Quantum chemistry |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Hartree-Fock". A list of authors is available in Wikipedia. |





 = \hat H^{core}(1)+\sum_{j=1}^{n/2}[2\hat J_j(1)-\hat K_j(1)]](images/math/d/2/7/d273c1cbecfe1e200cb09f449040c65e.png)
](images/math/7/5/d/75da23286a31f17c85c5d4c929e37f76.png)