To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
MomentumThe effect of motion is called momentum. In classical mechanics, momentum (pl. momenta; SI unit kg m/s, or, equivalently, N·s) is the product of the mass and velocity of an object. For more accurate measures of momentum, see the section "modern definitions of momentum" on this page. It is sometimes referred to as linear momentum to distinguish it from the related subject of angular momentum. Linear momentum is a vector quantity, since it has a direction as well as a magnitude. Momentum is a conserved quantity, meaning that the total momentum of any closed system (one not affected by external forces) cannot change. The concept of momentum in classical mechanics was originated by a number of great thinkers and experimentalists. The first of these was Ibn Sina (Avicenna) circa 1000, who referred to impetus as proportional to weight times velocity.[1] René Descartes later referred to mass times velocity as the fundamental force of motion. Galileo in his Two New Sciences used the term "impeto" (Italian), while Newton's Laws of Motion uses motus (Latin), which has been interpreted by subsequent scholars to mean momentum.[citation needed] Product highlight
Newtonian mechanicsIf an object is moving in any reference frame, then it has momentum in that frame. It is important to note that momentum is frame dependent. That is, the same object may have a certain momentum in one frame of reference, but a different amount in another frame. For example, a moving object has momentum in a reference frame fixed to a spot on the ground, while at the same time having 0 momentum in a reference frame attached to the object's center of mass. The amount of momentum that an object has depends on two physical quantities: the mass and the velocity of the moving object in the frame of reference. In physics, the usual symbol for momentum is a small bold p (bold because it is a vector); so this can be written: where:
(using bold text for vectors). The origin of the use of p for momentum is unclear. It has been suggested that, since m had already been used for mass, meter, and -milli, the p may be derived from the Latin petere ("to go") or from "progress" (a term used by Leibniz).[citation needed] The velocity of an object at a particular instant is given by its speed and the direction of its motion at that instant. Because momentum depends on and includes the physical quantity of velocity, it too has a magnitude and a direction and is a vector quantity. For example the momentum of a 5-kg bowling ball would have to be described by the statement that it was moving westward at 2 m/s. It is insufficient to say that the ball has 10 kg m/s of momentum because momentum is not fully described unless its direction is given. Momentum for a systemRelating to mass and velocityThe momentum of a system of objects is the vector sum of the momenta of all the individual objects in the system. where
It can be shown that, in the center of mass frame the momentum of a system is zero. Additionally, the momentum in a frame of reference that is moving at a speed where:
Relating to forceForce is equal to the rate of change of momentum:
In the case of constant mass, and velocities much less than the speed of light, this definition results in the equation If a system is in equilibrium, then the change in momentum with respect to time is equal to 0: Conservation of momentumThe law of conservation of momentum is a fundamental law of nature, and it states that the total momentum of a closed system of objects (which has no interactions with external agents) is constant. One of the consequences of this is that the centre of mass of any system of objects will always continue with the same velocity unless acted on by a force outside the system. Conservation of momentum is a mathematical consequence of the homogeneity (shift symmetry) of space (position in space is canonical conjugate quantity to momentum). So, momentum conservation can be philosophically stated as "nothing depends on location per se". In an isolated system (one where external forces are absent) the total momentum will be constant: this is implied by Newton's first law of motion. Newton's third law of motion, the law of reciprocal actions, which dictates that the forces acting between systems are equal in magnitude, but opposite in sign, is due to the conservation of momentum. Since position in space is a vector quantity, momentum (being canonical conjugate of position) is a vector quantity as well - it has direction. Thus, when a gun is fired, the final total momentum of the system (the gun and the bullet) is the vector sum of the momentums of these two objects. Assuming that the gun and bullet were at rest prior to firing (meaning the initial momentum of the system was zero), the final total momentum must also equal 0. In an isolated system with only two objects, the amount of momentum gained by one object must equal the loss of momentum by the other object. Mathematically,
Momentum has the special property that, in a closed system, it is always conserved, even in collisions and separations caused by explosive forces. Kinetic energy, on the other hand, is not conserved in collisions if they are inelastic. Since momentum is conserved it can be used to calculate an unknown velocity following a collision or a separation if all the other masses and velocities are known. A common problem in physics that requires the use of this fact is the collision of two particles. Since momentum is always conserved, the sum of the momenta before the collision must equal the sum of the momenta after the collision: where:
Usually, we either only know the velocities before or after a collision and would like to also find out the opposite. Correctly solving this problem means you have to know what kind of collision took place. There are two basic kinds of collisions, both of which conserve momentum:
Elastic collisionsA collision between two pool or snooker balls is a good example of an almost totally elastic collision. In addition to momentum being conserved when the two balls collide, the sum of kinetic energy before a collision must equal the sum of kinetic energy after: Since the 1/2 factor is common to all the terms, it can be taken out right away. Head-on collision (1 dimensional)In the case of two objects colliding head on we find that the final velocity which can then easily be rearranged to Special Case: m1>>m2 Now consider the case when the mass of one body, say m1, is far greater than that of the other, m2 (m1>>m2). In that case m1+m2 is approximately equal to m1 and m1-m2 is approximately equal to m1. Put these values in the above equation to calculate the value of v2 after collision. The expression changes to v2 final is 2*v1-v2. Its physical interpretation is in case of collision between two body one of which is very heavy, the lighter body moves with twice the velocity of the heavier body less its actual velocity but in opposite direction. Special Case: m1==m2 Another special case is when the collision is between two bodies of equal mass. Say body m1 moving at velocity v1 strikes body m2 that is at rest (v2). Putting this case in the equation derived above we will see that after the collision, the body that was moving (m1) will start moving with velocity v2 and the mass m2 will start moving with velocity v1. So there will be an exchange of velocities. Now suppose one of the masses, say m2, was at rest. In that case after the collision the moving body, m1, will come to rest and the body that was at rest, m2, will start moving with the velocity that m1 had before the collision. Note that all of these observations are for an elastic collision. This phenomenon is demonstrated by Newton's cradle, one of the best known examples of conservation of momentum, a real life example of this special case. Multi-dimensional collisionsIn the case of objects colliding in more than one dimension, as in oblique collisions, the velocity is resolved into orthogonal components with one component perpendicular to the plane of collision and the other component or components in the plane of collision. The velocity components in the plane of collision remain unchanged, while the velocity perpendicular to the plane of collision is calculated in the same way as the one-dimensional case. For example, in a two-dimensional collision, the momenta can be resolved into x and y components. We can then calculate each component separately, and combine them to produce a vector result. The magnitude of this vector is the final momentum of the isolated system. See the elastic collision page for more details. x = 2a Inelastic collisionsA common example of a perfectly inelastic collision is when two snowballs collide and then stick together afterwards. This equation describes the conservation of momentum: It can be shown that a perfectly inelastic collision is one in which the maximum amount of kinetic energy is converted into other forms. For instance, if both objects stick together after the collision and move with a final common velocity, one can always find a reference frame in which the objects are brought to rest by the collision and 100% of the kinetic energy is converted. This is true even in the relativistic case and utilized in particle accelerators to efficiently convert kinetic energy into new forms of mass-energy (i.e. to create massive particles). In case of Inelastic collision, there is a parameter attached called coefficient of restitution (denoted by small 'e'or 'c' in many text books). It is defined as the ratio of relative velocity of separation to relative velocity of approach. It is a ratio hence it is a dimensionless quantity. When we have an elastic collision the value of e (= coefficient of restitution) is 1, i.e. the relative velocity of approach is same as the relative velocity of separation of the colliding bodies. In an elastic collision the Kinetic energy of the system is conserved. When a collision is not elastic (e<1) it is an inelastic collision. In case of a perfectly inelastic collision the relative velocity of separation of the centre of masses of the colliding bodies is 0. Hence after collision the bodies stick together after collision. In case of an inelastic collision the loss of Kinetic energy is maximum as stated above. In all types of collision if no external force is acting on the system of colliding bodies, the momentum will always get preserved.
Modern definitions of momentumMomentum in relativistic mechanicsIn relativistic mechanics, in order to be conserved, momentum must be defined as: where
Relativistic momentum becomes Newtonian momentum:
Relativistic four-momentum as proposed by Albert Einstein arises from the invariance of four-vectors under Lorentzian translation. The four-momentum is defined as: where
The "length" of the vector is the mass times the speed of light, which is invariant across all reference frames:
Momentum of massless objects Objects without a rest mass, such as photons, also carry momentum. The formula is: where
Generalization of momentum Momentum is the Noether charge of translational invariance. As such, even fields as well as other things can have momentum, not just particles. However, in curved space-time which is not asymptotically Minkowski, momentum isn't defined at all. Momentum in quantum mechanicsIn quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once. In quantum mechanics, position and momentum are conjugate variables. For a single particle with no electric charge and no spin, the momentum operator can be written in the position basis as where:
This is a commonly encountered form of the momentum operator, though not the most general one. Momentum in electromagnetismElectric and magnetic fields possess momentum regardless of whether they are static or they change in time. It is a great surprise for freshmen who are introduced to the well known fact of the pressure P of an electrostatic (magnetostatic) field upon a metal sphere, cylindrical capacity or ferromagnetic bar: where W,
Light (visible, UV, radio) is an electromagnetic wave and also has momentum. Even though photons (the particle aspect of light) have no mass, they still carry momentum. This leads to applications such as the solar sail. Momentum is conserved in an electrodynamic system (it may change from momentum in the fields to mechanical momentum of moving parts). The treatment of the momentum of a field is usually accomplished by considering the so-called energy-momentum tensor and the change in time of the Poynting vector integrated over some volume. This is a tensor field which has components related to the energy density and the momentum density. The definition canonical momentum corresponding to the momentum operator of quantum mechanics when it interacts with the electromagnetic field is, using the principle of least coupling:
instead of the customary
where:
Figurative useA process may be said to gain momentum. The terminology implies that it requires effort to start such a process, but that it is relatively easy to keep it going. Alternatively, the expression can be seen to reflect that the process is adding adherents, or general acceptance, and thus has more mass at the same velocity; hence, it gained momentum. See also
Notes
References
Categories: Continuum mechanics | Materials science |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Momentum". A list of authors is available in Wikipedia. |





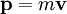
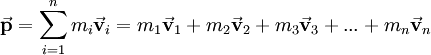
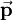 is the momentum
is the momentum
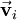 the vector velocity of object i
the vector velocity of object i
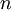 is the number of objects in the system
is the number of objects in the system
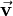 with respect to that frame is simply:
with respect to that frame is simply:
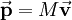
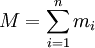 .
.
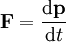 .
.
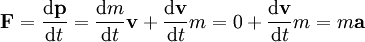 , commonly known as Newton's second law.
, commonly known as Newton's second law.
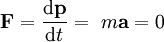
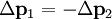
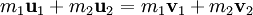
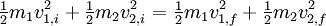
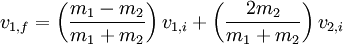
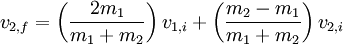
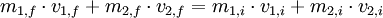
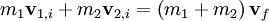
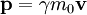
 is the invariant mass of the object moving,
is the invariant mass of the object moving,
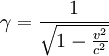 is the Lorentz factor
is the Lorentz factor
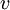 is the relative velocity between an object and an observer
is the relative velocity between an object and an observer
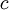 is the
is the 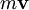 at low speed
at low speed 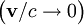 .
.
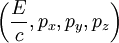
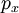 is the
is the 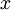 component of the relativistic momentum,
component of the relativistic momentum,
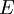 is the total energy of the system:
is the total energy of the system:
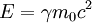
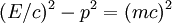
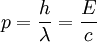
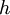 is Planck's constant,
is Planck's constant,
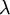 is the wavelength of the photon,
is the wavelength of the photon,
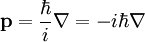
 is the gradient operator
is the gradient operator
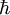 is the reduced Planck constant.
is the reduced Planck constant.
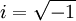 is the imaginary unit.
is the imaginary unit.
![P_{static} = {W}= [ {\epsilon_0 \epsilon}{\frac{{\mathbf E}^2 }{ {2}}} +{\frac{ 1 }{ {\mu_0 \mu} }} {\frac{{\mathbf B}^2}{{2}}}],](images/math/6/9/0/690488566c244c4209b835f82125fc76.png)
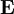 ,
, 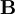 ,
are electromagnetic energy density , electric and magnetic fields respectively.
The electromagnetic pressure
,
are electromagnetic energy density , electric and magnetic fields respectively.
The electromagnetic pressure 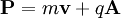 ,
,
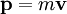 ,
,
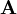 is the electromagnetic vector potential
is the electromagnetic vector potential
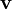 its velocity
its velocity


