To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Poynting vectorIn physics, the Poynting vector can be thought of as representing the energy flux (W/m2) of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside independently co-discovered the Poynting vector. Usually, it is defined as where E is the electric field, H the auxiliary magnetic field, B the magnetic field, μ0 the permeability of vacuum, and μr the dimensionless relative permeability of the surrounding medium. (All bold letters represent vectors.) For example, the Poynting vector within the dielectric insulator of a coaxial cable is nearly parallel to the wire axis (assuming no fields outside the cable) - so electric energy is flowing through the dielectric between the conductors. If the core conductor was replaced by a wire having significant resistance, then the Poynting vector would become tilted toward that wire, indicating that energy flows from the e/m field into the wire, producing resistive Joule heating in the wire. Product highlight
InterpretationThe Poynting vector appears in the energy-conservation law[1], or Poynting's theorem, where J is the current density and u is the electromagnetic energy density, where ε0 is the permittivity of free space and εr the relative dielectric constant of the medium. The first term in the right-hand side represents the net electromagnetic energy flow into a small volume, while the second term represents negative of the work done by electrical currents that are not necessarily converted into electromagnetic energy. The Poynting vector in electromagnetic wavesIn a propagating sinusoidal electromagnetic plane wave of a fixed frequency, the Poynting vector oscillates, always pointing in the direction of propagation. The time-averaged magnitude of the Poynting vector is where E0 is the maximum amplitude of the electric field and c is the speed of light. This time-averaged value is also called the irradiance or intensity I. DerivationIn an electromagnetic plane wave, and their time and position dependences are where ω is the frequency of the wave and In the last step, we used the equality Radiation pressureS divided by the square of the speed of light in a vacuum is the density of the linear momentum of the electromagnetic field. The time-averaged intensity 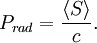 References
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Poynting_vector". A list of authors is available in Wikipedia. |


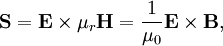



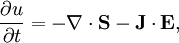
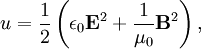
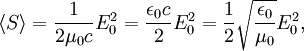
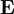 and
and 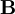 are always perpendicular to each other and the direction of propagation. Moreover, their amplitudes are related according to
are always perpendicular to each other and the direction of propagation. Moreover, their amplitudes are related according to
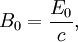
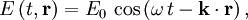
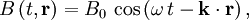
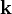 is wave vector.
The time-dependent and position magnitude of the Poynting vector is then
is wave vector.
The time-dependent and position magnitude of the Poynting vector is then
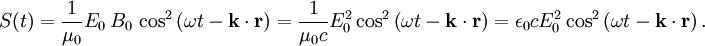
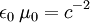 . Since the time- or space-average of
. Since the time- or space-average of 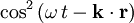 is
is  , it follows that
, it follows that
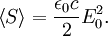
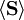 divided by the speed of light in a vacuum is the radiation pressure exerted by an electromagnetic wave on the surface of a target:
divided by the speed of light in a vacuum is the radiation pressure exerted by an electromagnetic wave on the surface of a target:

