My watch list
my.chemeurope.com  

my.chemeurope.com

With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.

  • My watch list
  • My saved searches
  • My saved topics
  • My newsletter
Register free of charge
Login  
eng  
DeutschEnglishFrançaisEspañol

Overlap matrix



The overlap matrix is a square matrix, used in quantum chemistry to describe the inter-relationship of a set of basis vectors of a quantum system. In particular, if the vectors are orthogonal to one another, the overlap matrix will be diagonal. In addition, if the basis vectors form an orthonormal set, the overlap matrix will be the identity matrix. The overlap matrix is always n×n, where n is the number of basis functions used. It is a kind of Gramian matrix.

In general, the overlap matrix is defined as:

\mathbf{S}_{jk}=\left \langle b_j|b_k \right \rangle=\int \Psi_j^* \Psi_k d\tau

where

\left |b_j \right \rangle

is the j-th basis ket (vector), and

Ψj

is the j-th wavefunction, defined as

\Psi_j(x)=\left \langle x | b_j \right \rangle.

See also

References

Quantum Chemistry: Fifth Edition, Ira N. Levine, 2000

 
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Overlap_matrix". A list of authors is available in Wikipedia.
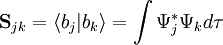
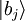
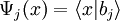Your browser is not current. Microsoft Internet Explorer 6.0 does not support some functions on Chemie.DE