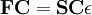To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Roothaan equationsThe Roothaan equations are a representation of the Hartree-Fock equation in a non orthonormal basis set which can be of Gaussian-type or Slater-type. It applies to closed-shell molecules or atoms where all molecular orbitals or atomic orbitals, respectively, are doubly occupied. This is generally called Restricted Hartree-Fock theory. Product highlightThe method was developed independently by Clemens C. J. Roothaan and George G. Hall in 1951, and is thus sometimes called the Roothaan-Hall equations. [1] [2] [3] The Roothaan equations can be written in the form of generalized eigenvalue problem Where F is the so-called Fock matrix, C is a matrix of coefficients, S is the overlap matrix of the basis functions, and ε is the (diagonal, by convention) matrix of orbital energies. In the case of an orthonormalised basis set the overlap matrix, S, reduces to the identity matrix. See alsoReferences |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Roothaan_equations". A list of authors is available in Wikipedia. |