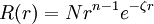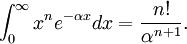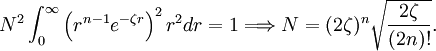To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Slater-type orbitalSlater-type orbitals (STOs) are functions used as atomic orbitals in the linear combination of atomic orbitals molecular orbital method. They are named after the physicist John C. Slater, who introduced them in 1930[1]. Product highlightSTOs have the following radial part: where
The normalization constant is computed from the integral Hence It is common to use the real form of spherical harmonics depending on the polar coordinates θ and φ as the angular part of the Slater orbital. References
See also |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Slater-type_orbital". A list of authors is available in Wikipedia. |