To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Atomic orbitalAn atomic orbital is a mathematical function that describes the wave-like behavior of an electron in an atom. The region in which an electron may be found around a single atom in a particular energy state can be calculated from this function. The term "orbital" has become known as either the "mathematical function" or the "region" generated with the function.[1] Specifically, atomic orbitals are the possible quantum states of an individual electron in the electron cloud around a single atom, as described by the function.
Classically, the electrons were thought to orbit the atomic nucleus, much like the planets around the Sun (or more accurately, a moth orbiting very quickly around a lamp). Explaining the behavior of the electrons that "orbit" an atom was one of the driving forces behind the development of quantum mechanics. In quantum mechanics, atomic orbitals are described as wave functions over space, indexed by the n, l, and m quantum numbers of the orbital or by the names as used in electron configurations, as shown on the right. As electrons cannot be described as solid particles (as a planet or a moth) in this way, a more accurate analogy would be that of a huge atmosphere, the spatially distributed electron, around a tiny planet which is the atomic nucleus. Hence the term "orbit" was substituted with something else: orbital. The orbital names (s, p, d, f, g, h,...) are derived from the characteristics of their spectroscopic lines: sharp, principal, diffuse and fundamental, the rest being named in alphabetical order. For mnemonic reasons, some call them spherical & peripheral. Product highlight
Orbital namesOrbitals are given names in the form: where X is the energy level corresponding to the principal quantum number n, type is a lower-case letter denoting the shape or subshell of the orbital and it corresponds to the angular quantum number l, and y is the number of electrons in that orbital. For example, the orbital 1s2 (pronounced "one ess two") has two electrons and is the lowest energy level (n = 1) and has an angular quantum number of l = 0. In some cases, the principal quantum number is given a letter associated with it. For n = 1, 2, 3, 4, 5 ....., the letters associated with those numbers are K, L, M, N, O .... respectively. Formal quantum mechanical definitionIn quantum mechanics, the state of an atom, i.e. the eigenstates of the atomic Hamiltonian, is expanded (see configuration interaction expansion and basis (linear algebra)) into linear combinations of anti-symmetrized products (Slater determinants) of one-electron functions. The spatial components of these one-electron functions are called atomic orbitals. (When one considers also their spin component, one speaks of atomic spin orbitals.) In atomic physics, the atomic spectral lines correspond to transitions (quantum leaps) between quantum states of an atom. These states are labelled by a set of quantum numbers summarized in the term symbol and usually associated to particular electron configurations, i.e. by occupations schemes of atomic orbitals (e.g. 1s2 2s2 2p6 for the ground state of neon -- term symbol: 1S0). This notation means that the corresponding Slater determinants have a clear higher weight in the configuration interaction expansion. The atomic orbital concept is therefore a key concept for visualizing the excitation process associated to a given transition. For example, one can say for a given transition that it corresponds to the excitation of an electron from an occupied orbital to a given unoccupied orbital. Nevertheless one has to keep in mind that electrons are fermions ruled by Pauli exclusion principle and cannot be distinguished from the other electrons in the atom. Moreover, it sometimes happens that the configuration interaction expansion converges very slowly and that one cannot speak about simple one-determinantal wave function at all. This is the case when electron correlation is large. Fundamentally, an atomic orbital is a one-electron wavefunction. Don't forget that when thinking about orbitals, we are often bombarded (even if we don't know it) by the Hartree-Fock vision of molecular orbital theory. Connection to uncertainty relationAfter Heisenberg discovered his rightly famous uncertainty relation it was discovered by men like Pauling amd Mulliken that the consequences were that the electron could no longer be considered as in an exact location in its orbital. Rather the electron had to be described by every point where the electron could possibly inhabit. By creating points of probable location for the electron in its known orbital, this created a cloud of points in a spherical shape for the orbital of a hydrogen atom which points gradually faded out nearer to the nucleus and farther from the nucleus. This is called a probability distribution. Therefore, the Bohr atom number n for each orbital became known as an n-sphere in the three dimensional atom and was pictured as a probability cloud where the electron surrounded the atom all at once. This led to the further description by Heisenberg that if a measurement of the electron was not being taken that it could not be described in one particular location but was everywhere in the electron cloud at once. In other words, quantum mechanics cannot give exact results, but only the probabilities for the occurrence of a variety of possible results. Heisenberg went further and said that the path of a moving particle only comes into existence once we observe it. However strange and counter-intuitive this assertion may seem, quantum mechanics does still tell us the location of the electron's orbital, its probability cloud. Heisenberg was speaking of the particle itself, not its orbital which is in a known probability distribution. It is important to note that although Heisenberg used infinite sets of positions for the electron in his matrices, this does not mean that the electron could be anywhere in the universe. Rather there are several laws that show the electron must be in one localized probability distribution. An electron is described by its energy in Bohr's atom which was carried over to matrix mechanics. Therefore, an electron in a certain n-sphere had to be within a certain range from the nucleus depending upon its energy. This restricts its location. Also, the number of places an electron can be is also called "the number of cells in its phase space". The Uncertainty Principle set a lower limit to how finely one can chop up classical phase space, so the number of places that an electron can be in its orbital becomes finite. An electron's location in an atom is defined to be in its orbital, but stops at the nucleus and before the next n-sphere orbital begins Hydrogen-like atomsThe simplest atomic orbitals are those that occur in an atom with a single electron, such as the hydrogen atom. In this case the atomic orbitals are the eigenstates of the hydrogen Hamiltonian. They can be obtained analytically (see hydrogen atom). An atom of any other element ionized down to a single electron is very similar to hydrogen, and the orbitals take the same form. For atoms with two or more electrons, the governing equations can only be solved with the use of methods of iterative approximation. Orbitals of multi-electron atoms are qualitatively similar to those of hydrogen, and in the simplest models, they are taken to have the same form. For more rigorous and precise analysis, the numerical approximations must be used. A given (hydrogen-like) atomic orbital is identified by unique values of three quantum numbers: n, l, and ml. The rules restricting the values of the quantum numbers, and their energies (see below), explain the electron configuration of the atoms and the periodic table. The stationary states (quantum states) of the hydrogen-like atoms are its atomic orbital. However, in general, an electron's behavior is not fully described by a single orbital. Electron states are best represented by time-depending "mixtures" (linear combinations) of multiple orbitals. See Linear combination of atomic orbitals molecular orbital method. The quantum number n first appeared in the Bohr model. It determines, among other things, the distance of the electron from the nucleus; all electrons with the same value of n lie at the same distance. Modern quantum mechanics confirms that these orbitals are closely related. For this reason, orbitals with the same value of n are said to comprise a "shell". Orbitals with the same value of n and also the same value of l are even more closely related, and are said to comprise a "subshell". Qualitative characterizationLimitations on the quantum numbersAn atomic orbital is uniquely identified by the values of the three quantum numbers, and each set of the three quantum numbers corresponds to exactly one orbital, but the quantum numbers only occur in certain combinations of values. The rules governing the possible values of the quantum numbers are as follows: The principal quantum number n is always a positive integer. In fact, it can be any positive integer, but for reasons discussed below, large numbers are seldom encountered. Each atom has, in general, many orbitals associated with each value of n; these orbitals together are sometimes called a shell. The azimuthal quantum number The magnetic quantum number The above results may be summarized in the following table. Each cell represents a subshell, and lists the values of
Subshells are usually identified by their n- and The shapes of orbitalsAny discussion of the shapes of electron orbitals is necessarily imprecise, because a given electron, regardless of which orbital it occupies, can at any moment be found at any distance from the nucleus and in any direction due to the uncertainty principle. However, the electron is much more likely to be found in certain regions of the atom than in others. Given this, a boundary surface can be drawn so that the electron has a high probability to be found anywhere within the surface, and all regions outside the surface have low values. The precise placement of the surface is arbitrary, but any reasonably compact determination must follow a pattern specified by the behavior of ψ2, the square of the wavefunction. This boundary surface is what is meant when the "shape" of an orbital is mentioned. Generally speaking, the number n determines the size and energy of the orbital: as n increases, the size of the orbital increases. Also in general terms, The single s-orbitals ( The three p-orbitals have the form of two ellipsoids with a point of tangency at the nucleus (sometimes referred to as a dumbbell). The three p-orbitals in each shell are oriented at right angles to each other, as determined by their respective values of Four of the five d-orbitals look similar, each with four pear-shaped balls, each ball tangent to two others, and the centers of all four lying in one plane, between a pair of axes. Three of these planes are the xy-, xz-, and yz-planes, and the fourth has the centres on the x and y axes. The fifth and final d-orbital consists of three regions of high probability density: a torus with two pear-shaped regions placed symmetrically on its z axis. There are seven f-orbitals, each with shapes more complex than those of the d-orbitals. The shapes of atomic orbitals in one-electron atom are related to 3-dimensional spherical harmonics. Orbitals tableThis table shows all orbital configurations up to 7s, therefore it covers the simple electronic configuration for all elements from the periodic table up to Ununbium (element 112) with the exception of Lawrencium (element 103), which would require a 7p orbital.
Orbital energyIn atoms with a single electron (essentially the hydrogen atom), the energy of an orbital (and, consequently, of any electrons in the orbital) is determined exclusively by n. The n = 1 orbital has the lowest possible energy in the atom. Each successively higher value of n has a higher level of energy, but the difference decreases as n increases. For high n, the level of energy becomes so high that the electron can easily escape from the atom. In atoms with multiple electrons, the energy of an electron depends not only on the intrinsic properties of its orbital, but also on its interactions with the other electrons. These interactions depend on the detail of its spatial probability distribution, and so the energy levels of orbitals depend not only on n but also on The energy sequence of the first 24 subshells is given in the following table. Each cell represents a subshell with n and
Electron placement and the periodic tableSeveral rules govern the placement of electrons in orbitals (electron configuration). The first dictates that no two electrons in an atom may have the same set of values of quantum numbers (this is the Pauli exclusion principle). These quantum numbers include the three that define orbitals, as well as s, or spin quantum number. Thus, two electrons may occupy a single orbital, so long as they have different values of s. However, only two electrons, because of their spin, can be associated with each orbital. Additionally, an electron always tends to fall to the lowest possible energy state. It is possible for it to occupy any orbital so long as it does not violate the Pauli exclusion principle, but if lower-energy orbitals are available, this condition is unstable. The electron will eventually lose energy (by releasing a photon) and drop into the lower orbital. Thus, electrons fill orbitals in the order specified by the energy sequence given above. This behavior is responsible for the structure of the periodic table. The table may be divided into several rows (called 'periods'), numbered starting with 1 at the top. The presently known elements occupy seven periods. If a certain period has number i, it consists of elements whose outermost electrons fall in the ith shell. The periodic table may also be divided into several numbered rectangular 'blocks'. The elements belonging to a given block have this common feature: their highest-energy electrons all belong to the same The number of electrons in a neutral atom increases with the atomic number. The electrons in the outermost shell, or valence electrons, tend to be responsible for an element's chemical behavior. Elements that contain the same number of valence electrons can be grouped together and display similar chemical properties. See also
References
Categories: Chemical bonding | Atomic physics |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Atomic_orbital". A list of authors is available in Wikipedia. |





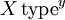
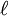 is a non-negative integer. Within a shell where n is some integer n0,
is a non-negative integer. Within a shell where n is some integer n0, 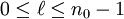 . For instance, the n = 1 shell has only orbitals with
. For instance, the n = 1 shell has only orbitals with 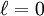 , and the n = 2 shell has only orbitals with
, and the n = 2 shell has only orbitals with 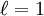 . The set of orbitals associated with a particular value of
. The set of orbitals associated with a particular value of 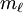 is also always an integer. Within a subshell where
is also always an integer. Within a subshell where 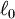 ,
, 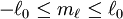 .
.


