Configuration interaction

Configuration interaction (CI) is a post Hartree-Fock linear variational method for solving the nonrelativistic Schrödinger equation within the Born-Oppenheimer approximation for a quantum chemical multi-electron system. Two meanings are connected to the term configuration interaction in this context. Mathematically, configuration simply describes the linear combination of Slater determinants used for the wave function. In terms of a specification of orbital occupation (for instance, (1s)²(2s)²(2p)¹...), interaction means the mixing (interaction) of different electronic configurations (states). Due to the long CPU time and immense hardware required for CI calculations, the method is limited to relatively small systems.

Additional recommended knowledge

Don't let static charges disrupt your weighing accuracy

Recognize and detect the effects of electrostatic charges on your balance

What is the Sensitivity of my Balance?

In contrast to the Hartree-Fock method, in order to account for electron correlation, CI uses a variational wave function that is a linear combination of configuration state functions (CSFs) built from spin orbitals (denoted by the superscript SO),

where Ψ is usually the electronic ground state of the system. If the expansion includes all possible CSFs of the appropriate symmetry, then this is a full configuration interaction procedure which exactly solves the electronic Schrödinger equation within the space spanned by the one-particle basis set. The first term in the above expansion is normally the Hartree-Fock determinant. The other CSFs can be characterised by the number of spin orbitals that are swapped with virtual orbitals from the Hartree-Fock determinant. If only one spin orbital differs, we describe this as a single excitation determinant. If two spin orbitals differ it is a double excitation determinant and so on. This is used to limit the number of determinants in the expansion. For example, the method CID is limited to double excitations only. The method CISD is limited to single and double excitations. Single excitations on their own do not mix with the Hartree-Fock determinant. These methods, CID and CISD, are in many standard programs. The Davidson correction can be used to estimate a correction to the CISD energy to account for higher excitations. When solving the CI equations, approximations to excited states are also obtained, which differ in the values of their coefficients c_I.

The CI procedure leads to a general matrix eigenvalue equation:

where c is the coefficient vector, e is the eigenvalue matrix, and the elements of the hamiltonian and overlap matrices are, respectively,

,

.

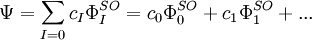
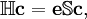
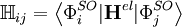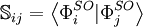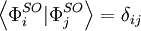Slater determinants are constructed from sets of orthonormal spin orbitals, so that , making 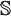the identity matrix and simplifying the above matrix equation.

See also

• Electron correlation
• Multireference configuration interaction
• Post Hartree-Fock
• Quantum chemistry

References

• Cramer, Christopher J. (2002). Essentials of Computational Chemistry. Chichester: John Wiley & Sons, Ltd., 191 - 232. ISBN 0-471-48552-7.