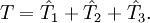To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Coupled cluster
Coupled cluster (CC) is a numerical technique used for describing many-body systems. Its most common use is as one of several quantum chemical post-Hartree-Fock ab initio quantum chemistry methods in the field of computational chemistry. It starts from the Hartree-Fock molecular orbital method and adds a correction term to take into account electron correlation. Some of the most accurate calculations for small to medium sized molecules use this method. The method was initially developed by Fritz Coester and Hermann Kümmel in the 1950s for studying nuclear physics phenomena, but became more frequently used after Jiři Čížek and Josef Paldus reformulated the method for electron correlation in atoms and molecules in the 1960s. It is now one of the most prevalent methods in quantum chemistry that includes electronic correlation. Product highlight
Wavefunction ansatzCoupled-cluster theory provides an approximate solution to the time-independent Schrödinger equation where The wavefunction of the coupled-cluster theory is written as an exponential ansatz:
where The choice of the exponential ansatz is opportune because (unlike other ansatzes, for example, configuration interaction) it guarantees the size extensivity of the solution. Size consistency in CC theory, however, depends on the size consistency of the reference wave function. Cluster operatorThe cluster operator is written in the form
where etc In the above formulae Taking into consideration the structure of This series is finite in practice because the number of occupied molecular orbitals is finite, as is the number of excitations. In order to simplify the task for finding the coefficients t, the expansion of then Slater determinants excited more than n times may (and usually do) still contribute to the wave function Coupled-cluster equationsCoupled-cluster equations are equations whose solution is the set of coefficients t. There are several ways of writing such equations but the standard formalism results in a terminating set of equations which may be solved iteratively. The naive variational approach does not take advantage of the connected nature of the cluster amplitudes and results in a non-terminating set of equations. Suppose there are q coefficients t to solve for. Therefore, we need q equations. It is easy to notice that each t-coefficient may be put in correspondence with a certain excited determinant: where by Unfortunately,
the latter being the equations to be solved and the former the equation for the evaluation of the energy. Consider the standard CCSD method:
which when reduced using the BCH formula for the similarity transformed Hamiltonian, Types of coupled-cluster methodsThe classification of traditional coupled-cluster methods rests on the highest number of excitations allowed in the definition of
Thus, the Terms in round brackets indicate that these terms are calculated based on perturbation theory. For example, a CCSD(T) approach simply means:
General description of the theoryThe complexity of equations and the corresponding computer codes, as well as the cost of the computation increases sharply with the highest level of excitation. For many applications the sufficient accuracy may be obtained with CCSD, and the more accurate (and more expensive) CCSD(T) is often called "the gold standard of quantum chemistry" for its excellent compromise between the accuracy and the cost for the molecules near equilibrium geometries. More complicated coupled-cluster methods such as CCSDT and CCSDTQ are used only for high-accuracy calculations of small molecules. The inclusion of all n levels of excitation for the n-electron system gives the exact solution of the Schrödinger equation within the given basis set. One possible improvement to the standard coupled-cluster approach is to add terms linear in the interelectronic distances through methods such as CCSD-R12. This improves the treatment of dynamical electron correlation by satisfying the Kato cusp condition and accelerates convergence with respect to the orbital basis set. Unfortunately, R12 methods invoke the resolution of the identity which requires a relatively large basis set in order to be valid. The coupled-cluster method described above is also known as the single-reference (SR) coupled-cluster method because the exponential ansatz involves only one reference function A historical accountIn the first reference below, Kümmel comments:
Relation to other theories
References
External resources
|
||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Coupled_cluster". A list of authors is available in Wikipedia. |





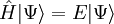
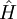 is the
is the 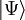 and E, respectively. Other variants of the coupled-cluster theory, such as equation-of-motion coupled cluster and multi-reference coupled cluster may also produce approximate solutions for the excited states of the system.
and E, respectively. Other variants of the coupled-cluster theory, such as equation-of-motion coupled cluster and multi-reference coupled cluster may also produce approximate solutions for the excited states of the system.
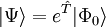 ,
,
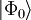 is a Slater determinant usually constructed from
is a Slater determinant usually constructed from 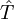 is an excitation operator which, when acting on
is an excitation operator which, when acting on 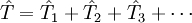 ,
,
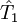 is the operator of all single excitations,
is the operator of all single excitations, 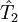 is the operator of all double excitations and so forth. In the formalism of second quantization these excitation operators are conveniently expressed as
is the operator of all double excitations and so forth. In the formalism of second quantization these excitation operators are conveniently expressed as
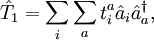
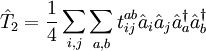
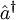 and
and 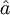 denote the creation and annihilation operators respectively and i, j stand for occupied and a, b for unoccupied orbitals. The creation and annihilation operators in the coupled cluster terms above are written in canonical form, where each term is in normal order. Being the one-particle excitation operator and the two-particle excitation operator,
denote the creation and annihilation operators respectively and i, j stand for occupied and a, b for unoccupied orbitals. The creation and annihilation operators in the coupled cluster terms above are written in canonical form, where each term is in normal order. Being the one-particle excitation operator and the two-particle excitation operator, 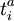 and
and 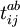 is necessary for finding the approximate solution
is necessary for finding the approximate solution 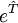 may be expanded into Taylor series:
may be expanded into Taylor series:
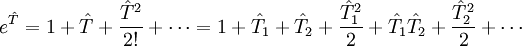
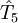 ,
, 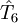 etc to the operator
etc to the operator 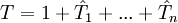
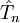 usually recovers more correlation energy than configuration interaction with maximum n excitations.
usually recovers more correlation energy than configuration interaction with maximum n excitations.
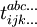 corresponds to the determinant obtained from
corresponds to the determinant obtained from 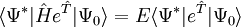
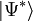 we understand the whole set of the appropriate excited determinants.
we understand the whole set of the appropriate excited determinants.
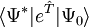 is a non-terminating sequence. The coupled-cluster equations are reduced to a closed form in the similarity transformed representation:
is a non-terminating sequence. The coupled-cluster equations are reduced to a closed form in the similarity transformed representation:
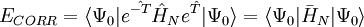 ,
,
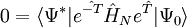 ,
,
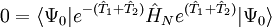 ,
,
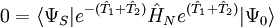 ,
,
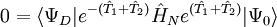 ,
,
![e^{\hat{-T}} \hat{H} e^{\hat{T}} = H + [H,T] + (1/2)[[H,T],T] + ...](images/math/f/f/a/ffa0ca40683364a985aad7bb96b1b3f1.png) , become quartic in
, become quartic in