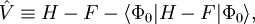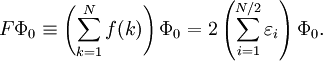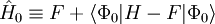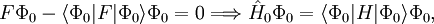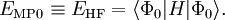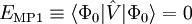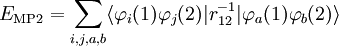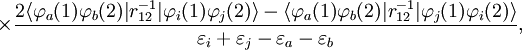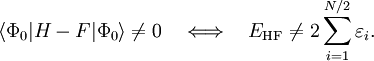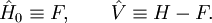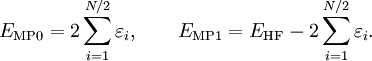To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Møller-Plesset perturbation theory
Møller-Plesset perturbation theory (MP) is one of several quantum chemistry post-Hartree-Fock ab initio methods in the field of computational chemistry. It improves on the Hartree-Fock method by adding electron correlation effects by means of Rayleigh-Schrödinger perturbation theory (RS-PT), usually to second (MP2), third (MP3) or fourth (MP4) order. Its main idea was published as early as 1934.[1] Product highlight
Rayleigh-Schrödinger perturbation theoryThe MP-theory is a special application of RS-PT. In RS-PT one considers an unperturbed Hamiltonian operator
where λ is an arbitrary real parameter. In MP-theory the zeroth-order wave function is an exact eigenfunction of the Fock operator, which thus serves as the unperturbed operator. The perturbation is the correlation potential. In RS-PT the perturbed wave function and perturbed energy are expressed as a power series in λ:
Substitution of these series into the time-independent Schrödinger equation gives a new equation: (
Equating the factors of λk in this equation gives an kth-order perturbation equation, where k=0,1,2, ..., n. Møller-Plesset perturbationOriginal formulationThe MP-energy corrections are obtained from Rayleigh-Schrödinger (RS) perturbation theory with the perturbation (correlation potential): where the normalized Slater determinant Φ0 is the lowest eigenfunction of the Fock operator Here N is the number of electrons of the molecule under consideration, H is the usual electronic Hamiltonian, f(1) is the one-electron Fock operator, and εi is the orbital energy belonging to the doubly occupied spatial orbital φi. The shifted Fock operator serves as the unperturbed (zeroth-order) operator. The Slater determinant Φ0 being an eigenfunction of F, it follows readily that so that the zeroth-order energy is the expectation value of H with respect to Φ0, i.e., the Hartree-Fock energy: Since the first-order MP energy is obviously zero, the lowest-order MP correlation energy appears in second order. This result is the Møller-Plesset theorem:[1] the correlation potential does not contribute in first-order to the exact electronic energy. In order to obtain the MP2 formula for a closed-shell molecule, the second order RS-PT formula is written on basis of doubly-excited Slater determinants. (Singly-excited Slater determinants do not contribute because of the Brillouin theorem). After application of the Slater-Condon rules for the simplification of N-electron matrix elements with Slater determinants in bra and ket and integrating out spin, it becomes where φi and φj are canonical occupied orbitals and φa and φb are canonical virtual orbitals. The quantities εi, εj, εa, and εb are the corresponding orbital energies. Clearly, through second-order in the correlation potential, the total electronic energy is given by the Hartree-Fock energy plus second-order MP correction: E ≈ EHF + EMP2. The solution of the zeroth-order MP equation (which by definition is the Hartree-Fock equation) gives the Hartree-Fock energy. The first non-vanishing perturbation correction beyond the Hartree-Fock treatment is the second-order energy. Alternative formulationEquivalent expressions are obtained by a slightly different partitioning of the Hamiltonian, which results in a different division of energy terms over zeroth- and first-order contributions, while for second- and higher-order energy corrections the two partitionings give identical results. The formulation is commonly used by chemists, who are now large users of these methods.[2] This difference is due to the fact, well-known in Hartree-Fock theory, that (The Hartree-Fock energy is not equal to the sum of occupied-orbital energies). In the alternative partitioning one defines, Clearly in this partioning, Obviously, the Møller-Plesset theorem does not hold in the sense that EMP1 ≠ 0. The solution of the zeroth-order MP equation is the sum of orbital energies. The zeroth plus first order correction yields the Hartree-Fock energy. As with the original formulation, the first non-vanishing perturbation correction beyond the Hartree-Fock treatment is the second-order energy. We reiterate that the second- and higher-order corrections are the same in both formulations. Use of Møller-Plesset perturbation methodsSecond (MP2), third (MP3), and fourth (MP4) order Møller-Plesset calculations are standard levels used in calculating small systems and are implemented in many computational chemistry codes. Higher level MP calculations, generally only MP5, are possible in some codes. However, they are rarely used because of their costs. Systematic studies of MP perturbation theory have shown that it is not necessarily a convergent theory at high orders. The convergence properties can be slow, rapid, oscillatory, regular, highly erratic or simply non-existent, depending on the precise chemical system or basis set.[3] Additionally, various important molecular properties calculated at MP3 and MP4 level are in no way better than their MP2 counterparts, even for small molecules.[4] For open shell molecules, MPn-theory can directly be applied only to unrestricted Hartree-Fock reference functions (since RHF states are not in general eigenvectors of the Fock operator). However, the resulting energies often suffer from severe spin contamination, leading to very wrong results. A much better alternative is to use one of the MP2-like methods based on restricted Hartree-Fock references. These methods, Hartree-Fock, unrestricted Hartree-Fock and restricted Hartree-Fock use a single determinant wave function. Multi-configurational self-consistent field methods use several determinants and can be used for the unperturbed operator, although not in a unique way so many methods, such as Complete Active Space Perturbation Theory (CASPT2) have been developed. See also
References
Further reading
|
||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Møller-Plesset_perturbation_theory". A list of authors is available in Wikipedia. |





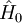 to which is added a small (often external) perturbation
to which is added a small (often external) perturbation 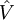 :
:
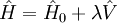 ,
,
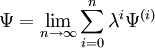 ,
,
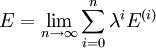 .
.
 )
)
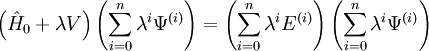 .
.