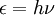To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Quantum chemistry
Quantum chemistry is a branch of theoretical chemistry, which applies quantum mechanics and quantum field theory to address issues and problems in chemistry. The description of the electronic behavior of atoms and molecules as pertaining to their reactivity is one of the applications of quantum chemistry. Quantum chemistry lies on the border between chemistry and physics, and significant contributions have been made by scientists from both fields. It has a strong and active overlap with the field of atomic physics and molecular physics, as well as physical chemistry. Quantum chemistry mathematically describes the fundamental behavior of matter at the molecular scale.[1] It is, in principle, possible to describe all chemical systems using this theory. In practice, only the simplest chemical systems may realistically be investigated in purely quantum mechanical terms, and approximations must be made for most practical purposes (e.g., Hartree-Fock, post Hartree-Fock or Density functional theory, see computational chemistry for more details). Hence a detailed understanding of quantum mechanics is not necessary for most chemistry, as the important implications of the theory (principally the orbital approximation) can be understood and applied in simpler terms. In quantum mechanics (several applications in computational chemistry and quantum chemistry), the Hamiltonian, or the physical state, of a particle can be expressed as the sum of two operators, one corresponding to kinetic energy and the other to potential energy. The Hamiltonian in the Schrödinger wave equation used in quantum chemistry does not contain terms for the spin of the electron. Solutions of the Schrödinger equation for the hydrogen atom gives the form of the wave function for atomic orbitals, and the relative energy of the 1s,2s,2p and 3s orbitals. The orbital approximation can be used to understand the other atoms e.g. helium, lithium and carbon. Product highlight
HistoryThe history of quantum chemistry began essentially with the 1838 discovery of cathode rays by Michael Faraday, the 1859 statement of the black body radiation problem by Gustav Kirchhoff, the 1877 suggestion by Ludwig Boltzmann that the energy states of a physical system could be discrete, and the 1900 quantum hypothesis by Max Planck that any energy radiating atomic system can theoretically be divided into a number of discrete ‘energy elements’ ε such that each of these energy elements is proportional to the frequency ν with which they each individually radiate energy, as defined by the following formula: where h is a numerical value called Planck’s Constant. Then, in 1905, to explain the photoelectric effect (1839), i.e. that shining light on certain materials can function to eject electrons from the material, Albert Einstein postulated, as based on Planck’s quantum hypothesis, that light itself consists of individual quantum particles, which later came to be called photons (1926). In the years to follow, this theoretical basis slowly began to be applied to chemical structure, reactivity, and bonding. Electronic structureThe first step in solving a quantum chemical problem is usually solving the Schrödinger equation (or Dirac equation in relativistic quantum chemistry) with the electronic molecular Hamiltonian. This is called determining the electronic structure of the molecule. It can be said that the electronic structure of a molecule or crystal implies essentially its chemical properties. Wave modelThe foundation of quantum mechanics and quantum chemistry is the wave model, in which the atom is a small, dense, positively charged nucleus surrounded by electrons. Unlike the earlier Bohr model of the atom, however, the wave model describes electrons as "clouds" moving in orbitals, and their positions are represented by probability distributions rather than discrete points. The strength of this model lies in its predictive power. Specifically, it predicts the pattern of chemically similar elements found in the periodic table. The wave model is so named because electrons exhibit properties (such as interference) traditionally associated with waves. See wave-particle duality. Valence bondAlthough the mathematical basis of quantum chemistry had been laid by Schrödinger in 1926, it is generally accepted that the first true calculation in quantum chemistry was that of the German physicists Walter Heitler and Fritz London on the hydrogen (H2) molecule in 1927. Heitler and London's method was extended by the American theoretical physicist John C. Slater and the American theoretical chemist Linus Pauling to become the Valence-Bond (VB) [or Heitler-London-Slater-Pauling (HLSP)] method. In this method, attention is primarily devoted to the pairwise interactions between atoms, and this method therefore correlates closely with classical chemists' drawings of bonds. Molecular orbitalAn alternative approach was developed in 1929 by Friedrich Hund and Robert S. Mulliken, in which electrons are described by mathematical functions delocalized over an entire molecule. The Hund-Mulliken approach or molecular orbital (MO) method is less intuitive to chemists, but has turned out capable of predicting spectroscopic properties better than the VB method. This approach is the conceptional basis of the Hartree-Fock method and further post Hartree-Fock methods. Density functional theoryThe Thomas-Fermi model was developed independently by Thomas and Fermi in 1927. This was the first attempt to describe many-electron systems on the basis of electronic density instead of wave functions, although it was not very successful in the treatment of entire molecules. The method did provide the basis for what is now known as density functional theory. Though this method is less developed than post Hartree-Fock methods, its lower computational requirements allow it to tackle larger polyatomic molecules and even macromolecules, which has made it the most used method in computational chemistry at present. Chemical dynamicsA further step can consist of solving the Schrödinger equation with the total molecular Hamiltonian in order to study the motion of molecules. Direct solution of the Schrödinger equation is called quantum molecular dynamics, within the semiclassical approximation semiclassical molecular dynamics, and within the classical mechanics framework molecular dynamics (MD). Statistical approaches, using for example Monte Carlo methods, are also possible. Adiabatic chemical dynamics
In adiabatic dynamics, interatomic interactions are represented by single scalar potentials called potential energy surfaces. This is the Born-Oppenheimer approximation introduced by Born and Oppenheimer in 1927. Pioneering applications of this in chemistry were performed by Rice and Ramsperger in 1927 and Kassel in 1928, and generalized into the RRKM theory in 1952 by Marcus who took the transition state theory developed by Eyring in 1935 into account. These methods enable simple estimates of unimolecular reaction rates from a few characteristics of the potential surface. Non-adiabatic chemical dynamicsNon-adiabatic dynamics consists of taking the interaction between several coupled potential energy surface (corresponding to different electronic quantum states of the molecule). The coupling terms are called vibronic couplings. The pioneering work in this field was done by Stueckelberg, Landau, and Zener in the 1930s, in their work on what is now known as the Landau-Zener transition. Their formula allows the transition probability between two diabatic potential curves in the neighborhood of an avoided crossing to be calculated. Quantum chemistry and quantum field theoryThe application of quantum field theory (QFT) to chemical systems and theories has become increasingly common in the modern physical sciences. One of the first and most fundamentally explicit appearances of this is seen in the theory of the photomagneton. In this system, plasmas, which are ubiquitous in both physics and chemistry, are studied in order to determine the basic quantization of the underlying bosonic field. However, quantum field theory is of interest in many fields of chemistry, including: nuclear chemistry, astrochemistry, sonochemistry, and quantum hydrodynamics. Field theoretic methods have also been critical in developing the ab initio Effective Hamiltonian theory of semi-empirical pi-electron methods. See also
Further reading
Nobel lectures by quantum chemists
References
Categories: Quantum chemistry | Theoretical chemistry |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Quantum_chemistry". A list of authors is available in Wikipedia. |