To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Bohr modelIn atomic physics, the Bohr model depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus — similar in structure to the solar system, but with electrostatic forces providing attraction, rather than gravity. This was an improvement on the earlier cubic model (1902), the plum-pudding model (1904), the Saturnian model (1904), and the Rutherford model (1911). Since the Bohr model is a quantum-physics based modification of the Rutherford model, many sources combine the two, referring to the Rutherford-Bohr model. Introduced by Niels Bohr in 1913, the model's key success lay in explaining the Rydberg formula for the spectral emission lines of atomic hydrogen; while the Rydberg formula had been known experimentally, it did not gain a theoretical underpinning until the Bohr model was introduced. Not only did the Bohr model explain the reason for the structure of the Rydberg formula, but it provided a justification for its empirical results in terms of fundamental physical constants. The Bohr model is a primitive model of the hydrogen atom. As a theory, it can be derived as a first-order approximation of the hydrogen atom using the broader and much more accurate quantum mechanics, and thus may be considered to be an obsolete scientific theory. However, because of its simplicity, and its correct results for selected systems (see below for application), the Bohr model is still commonly taught to introduce students to quantum mechanics, before moving on to the more accurate but more complex valence shell atom. A related model was originally proposed by Arthur Erich Haas in 1910, but was rejected. Product highlight
HistoryIn the early 20th century, experiments by Ernest Rutherford established that atoms consisted of a diffuse cloud of negatively charged electrons surrounding a small, dense, positively charged nucleus. Given this experimental data, it was quite natural for Rutherford to consider a planetary model for the atom, the Rutherford model of 1911, with electrons orbiting a sun-like nucleus. However, the planetary model for the atom has a difficulty. The laws of classical mechanics, specifically the Larmor formula, predict that the electron will release electromagnetic radiation as it orbits a nucleus. Because the electron would be losing energy, it would gradually spiral inwards and collapse into the nucleus. This is a disaster, because it predicts that all matter is unstable. Also, as the electron spirals inward, the emission would gradually increase in frequency as the orbit got smaller and faster. This would produce a continuous smear, in frequency, of electromagnetic radiation. However, late 19th century experiments with electric discharges through various low-pressure gasses in evacuated glass tubes had shown that atoms will only emit light (that is, electromagnetic radiation) at certain discrete frequencies. To overcome this difficulty, Niels Bohr proposed, in 1913, what is now called the Bohr model of the atom. He suggested that electrons could only have certain motions:
The significance of the Bohr model is that it states that the laws of classical mechanics do not apply to the motion of the electron about the nucleus. Bohr proposed rather that a new kind of mechanics, or quantum mechanics, describes the motion of the electrons around the nucleus. This model of electrons traveling in quantized orbits was extended into a more accurate model of electron motion about a dozen years later by Werner Heisenberg.Another form of the same theory, modern quantum mechanics, was discovered by the Austrian physicist Erwin Schrödinger independently and by different reasoning. Other points are:
Since the frequency of a photon is proportional to its energy, rule 2 allowed Bohr to calculate the gap in energy between levels--- the level spacing is equal to Planck's constant divided by the classical orbit period. Stepping down orbit by orbit, he found that the angular momentum changed by h / 2π at every step. So he proposed that the angular momentum L is quantized according to the rule where n = 1,2,3,… and is called the principal quantum number, and h is Planck's constant. The lowest value of n is 1. This corresponds to a smallest possible radius of 0.0529 nm. This is known as the Bohr radius. Once an electron is in this lowest orbit, it can get no closer to the proton. Bohr's condition, that the angular momentum is an integer multiple of Substituting DeBroglie's wavelength reproduces Bohr's rule. Bohr justified his rule by appealing to the correspondence principle, without providing a wave interpretation. Electron energy levelsThe Bohr model gives almost exact results only for a system where two charged points orbit each other at speeds much less than that of light. This not only includes one-electron systems such as the hydrogen atom, singly-ionized helium, doubly ionized lithium, but it includes positronium and Rydberg states of any atom where one electron is far away from everything else. It can be used for K-line X-ray transition calculations if other assumptions are added (see Moseley's law below). In high energy physics, it can be used to calculate the masses of heavy quark mesons. To calculate the orbits requires two assumptions: 1. The electron is held in a circular orbit by electrostatic attraction. The centripetal force is the Coulomb force.
2. The angular momentum of the circular orbit L = mvr is an integer multiple of
So an electron in the lowest energy level of hydrogen (n = 1) has -13.606 eV less energy than a motionless electron infinitely far from the nucleus. The next energy level at (n = 2) is -3.4 eV. The third (n = 3) is -1.51 eV, and so on. For larger values of n, these are also the binding energies of a highly excited atom with one electron in a large circular orbit around the rest of the atom. The combination of natural constants in the energy formula is called the Rydberg energy RE: This expression is clarified by interpreting it in combinations which form more natural units:
For nuclei with Z protons, the energy levels are:
When Z is approximately 100, the motion becomes highly relativistic. Then the Z2 cancels the α2 in R, so the orbit energy is comparable to rest energy. Sufficiently large nuclei, if they were stable, would reduce their charge by creating a bound electron from the vacuum, ejecting the positron to infinity. This is the theoretical phenomenon of electromagnetic charge screening which predicts a maximum nuclear charge. For positronium, the formula uses the reduced mass. For any value of the radius, the electron and the positron are each moving at half the speed around their common center of mass, and each has only one fourth the kinetic energy. The total kinetic energy is half what it would be for a single electron moving around a heavy nucleus.
Rydberg formulaThe Rydberg formula, which was known empirically before Bohr's formula, is now in Bohr's theory seen as describing the energies of transitions or quantum jumps between one orbital energy level, and another. Bohr's formula gives the numerical value of the already-known and measured Rydberg's constant, but now in terms of more fundamental constants of nature, including the electron's charge and Planck's constant. When the electron moves from one energy level to another, a photon is emitted. Using the derived formula for the different 'energy' levels of hydrogen one may determine the 'wavelengths' of light that a hydrogen atom can emit. The energy of a photon emitted by a hydrogen atom is given by the difference of two hydrogen energy levels: where nf is the final energy level, and ni is the initial energy level. Since the energy of a photon is the wavelength of the photon given off is given by This is known as the Rydberg formula, and the Rydberg constant R is RE / hc, or RE / 2π in natural units. This formula was known in the nineteenth century to scientists studying spectroscopy, but there was no theoretical explanation for this form or a theoretical prediction for the value of R, until Bohr. In fact, Bohr's derivation of the Rydberg constant was one reason that his model was immediately accepted. Shell Model of the AtomBohr extended the model of Hydrogen to give an approximate model for heavier atoms. This gave a physical picture which reproduced many known atomic properties for the first time. Heavier atoms have more protons in the nucleus, and more electrons to cancel the charge. Bohr's idea was that each discrete orbit could only hold a certain number of electrons. After that orbit is full, the next level would have to be used. This gives the atom a shell structure, in which each shell corresponds to a Bohr orbit. This model is even more approximate than the model of hydrogen, because it treats the electrons in each shell as non-interacting. But the repulsions of electrons is taken into account somewhat by the phenomenon of screening. The electrons in outer orbits do not only orbit the nucleus, but they also orbit the inner electrons, so the effective charge Z that they see is reduced by the number of the electrons in the inner orbit. For example, the lithium atom has two electrons in the lowest orbit, and these are orbiting at Z=2, since they see the whole nuclear charge of Z=3, minus the screening effect of the single innermost 1s electron. They thus, in simple theory, orbit at 1/4th the Bohr radius. The outer electron in lithium orbits at roughly Z=1, since the two electrons reduce the charge by 2. This outer electron should be at nearly one Bohr radius from the nucleus [However, the numbers do not come close to being integers in this fashion, save for large atoms and for the case of the Moseley's Law atom, in which innermost electrons do see a nuclear clarge of close to Z-1, and the outermost electron does see a charge of nearly 1]. In most other cases only electrons in the very innermost and the very outermost orbitals see a nuclear charge Z modified by a whole number. The shell model was able to qualitatively explain many of the mysterious properties of atoms which became codified in the late 19th century in the periodic table of the elements. One property was the size of atoms, which could be determined approximately by measuring the viscosity of gasses and density of pure crystaline solids. Atoms tend to get smaller as you move to the right in the periodic table, becoming much bigger at the next line of the table. Atoms to the right of the table tend to gain electrons, while atoms to the left tend to lose them. Elements at the end are chemically inert. In the shell model, this phenomenon is explained by shell-filling. Successive atoms get smaller because they are filling orbits of the same size, until the orbit is full-- at which point the next atom in the table has a loosely bound outer electron, causing it to expand. The first Bohr orbit is filled when it has two electrons, and this explains why helium is inert. The second orbit allows eight electrons, and when it is full the atom is neon, again inert. The third orbital contains eight again, except that in the more correct Sommerfeld treatment (reproduced in modern quantum mechanics) there are extra "d" electrons. The third orbit may hold an extra 10 d electrons, but these positions are not filled until a few more orbitals from the next level are filled (Filling the n=3 d orbitals produces the 10 transition elements). The irregular filling pattern is an effect of interactions between electrons, which are not taken into account in either the Bohr or Sommerfeld models, and which are difficult to calculate even in the modern treatment. Moseley's law and calculation of K-alpha X-ray emission linesNiels Bohr said in 1962, "You see actually the Rutherford work [the nuclear atom] was not taken seriously. We cannot understand today, but it was not taken seriously at all. There was no mention of it any place. The great change came from Moseley." In 1913 Henry Moseley found an empirical relationship between the strongest X-ray line emitted by atoms under electron bombardment (then known as the K-alpha line), and their atomic number Z. Moseley's empiric formula was found to be derivable from Rydberg and Bohr's formula (Moseley actually mentions only Ernest Rutherford and Antonius Van den Broek in terms of models). The two additional assumptions that [1] this X-ray line came from a transition between energy levels with quantum numbers 1 and 2, and [2], that the atomic number Z when used in the formula for atoms heavier than hydrogen, should be diminished by 1, to (Z-1)². Moseley wrote to Bohr, puzzled about his results, but Bohr was not able to help. At that he thought that the postulated innermost "K" shell of electrons should have at least four electrons, not two. So Moseley published his results without a theoretical explanation. Later, people realized that the effect was caused by charge screening. In the experiment, one of the innermost electrons in the atom is knocked out, leaving a vacancy in the lowest Bohr orbit. This vacancy is then filled by electrons in the next orbit, which has n=2. But the n=2 electrons see an effective charge of Z-1, which is also for some reason the value appropriate for the charge of the nucleus in the lowest Bohr orbit when 1 electron is already there. The energy gained by an electron dropping from the second shell to the first gives Moseley's law for K-alpha lines: or This latter relationship had been empirically derived by Moseley, in a simple plot of the square root of X-ray frequency against atomic number. Moseley's law not only established the objective meaning of atomic number (see Henry Moseley for detail) but, as Bohr noted, it also did more than the Rydberg derivation to establish the validity of the Rutherford/Van den Broek/Bohr nuclear model of the atom, with atomic number as nuclear charge. The K-alpha line of Moseley's time is now known to be a pair of close lines, written as (Kα1 and Kα2) in Siegbahn notation. ShortcomingsThe Bohr model gives an incorrect value In modern quantum mechanics, the electron in hydrogen is a spherical cloud of probability which grows more dense near the nucleus. The rate of decay in hydrogen is equal to the Bohr radius, but since Bohr worked with circular orbits, not zero area ellipses, the fact that these two numbers exactly agree is a coincidence. The Bohr model also has difficulty with, or else fails to explain:
RefinementsSeveral enhancements to the Bohr model were proposed; most notably the Sommerfeld model or Bohr-Sommerfeld model, which suggested that electrons travel in elliptical orbits around a nucleus instead of the Bohr model's circular orbits. This model supplemented the quantized angular momentum condition of the Bohr model with an additional radial quantization condition, the Sommerfeld-Wilson quantization condition where p is the momentum canonically conjugate to the coordinate q; the integral is the action of action-angle coordinates. This condition is the only one possible, since the quantum numbers are adiabatic invariants. The Bohr-Sommerfeld model was fundamentally inconsistent and led to many paradoxes. The azimuthal quantum number measured the tilt of the orbital plane relative to the x-y plane, and it could only take a few discrete values. This contradicted the obvious fact that an atom could be turned this way and that relative to the coordinates without restriction. The Sommerfeld quantization can be performed in different canonical coordinates, and gives answers which are different. The incorporation of radiation corrections was difficult, because it required finding action-angle coordinates for a combined radiation/atom system, which is difficult when the radiation is allowed to escape. The whole theory did not extend to non-integrable motions, which meant that many systems could not be treated even in principle. In the end, the model was replaced the modern quantum mechanical treatment of the hydrogen atom, which was first given by Wolfgang Pauli in 1925, using Heisenberg's matrix mechanics. The current picture of the hydrogen atom is based on the atomic orbitals of wave mechanics which Erwin Schrodinger developed in 1926. However, this is not to say that the Bohr model was without its successes. Calculations based on the Bohr-Sommerfeld model were able to accurately explain a number of more complex atomic spectral effects. For example, up to first-order perturbation, the Bohr model and quantum mechanics make the same predictions for the spectral line splitting in the Stark effect. At higher-order perturbations, however, the Bohr model and quantum mechanics differ, and measurements of the Stark effect under high field strengths helped confirm the correctness of quantum mechanics over the Bohr model. The prevailing theory behind this difference lies in the shapes of the orbitals of the electrons, which vary in shape according to the energy state of the electron. The Bohr-Sommerfeld quantization conditions lead to questions in modern mathematics. Consistent semiclassical quantization condition requires a certain type of structure on the phase space, which places topological limitations on the types of symplectic manifolds which can be quantized. In particular, the symplectic form should be the curvature form of a connection of a Hermitian line bundle, which is called a prequantization. See also
ReferencesHistorical
Further reading
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Bohr_model". A list of authors is available in Wikipedia. |





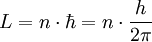
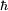 was later reinterpreted by DeBroglie as a standing wave condition: the electron is described by a wave and a whole number of wavelengths must fit along the circumference of the electron's orbit.
was later reinterpreted by DeBroglie as a standing wave condition: the electron is described by a wave and a whole number of wavelengths must fit along the circumference of the electron's orbit.
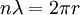
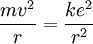
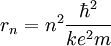
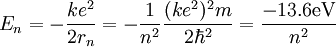
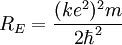
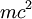 : the rest energy of the electron
: the rest energy of the electron
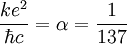 : the fine structure constant
: the fine structure constant
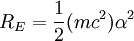
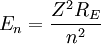 (Heavy Nuclei)
(Heavy Nuclei)
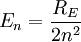 (Positronium)
(Positronium)
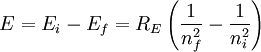
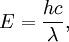
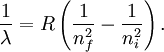
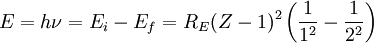
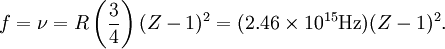
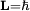 for the ground state orbital angular momentum. The angular momentum in the true ground state is known to be zero. Although mental pictures fail somewhat at these levels of scale, an electron in the lowest modern "orbital" with no orbital momentum, may be thought of as not to rotate "around" the nucleus at all, but merely to go tightly around it in an ellipse with zero area. This is only reproduced in a more sophisticated semiclassical treatment like Sommerfeld's.
for the ground state orbital angular momentum. The angular momentum in the true ground state is known to be zero. Although mental pictures fail somewhat at these levels of scale, an electron in the lowest modern "orbital" with no orbital momentum, may be thought of as not to rotate "around" the nucleus at all, but merely to go tightly around it in an ellipse with zero area. This is only reproduced in a more sophisticated semiclassical treatment like Sommerfeld's.


