To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Bohr radius
In the Bohr model of the structure of an atom, put forward by Niels Bohr in 1913, electrons orbit a central nucleus. The model says that the electrons orbit only at certain distances from the nucleus, depending on their energy. In the simplest atom, hydrogen, a single electron orbits, and the smallest possible orbit for the electron, that with the lowest energy, is most likely to be found at a distance from the nucleus called the Bohr radius. Product highlightAccording to 2002 CODATA, the Bohr radius of hydrogen has a value of 5.291772108(18)×10−11 m (i.e., approximately 53 pm or 0.53 ångströms). The number in parentheses (18) denotes the uncertainty of the last digits. This value can be computed in terms of other physical constants:
where:
While the Bohr model does not correctly describe an atom, the Bohr radius keeps its physical meaning as a characteristic size of the electron cloud in a full quantum-mechanical description. Thus the Bohr radius is often used as a unit in atomic physics, see atomic units. Note that the definition of Bohr radius does not include the effect of reduced mass, and so it is not precisely equal to the orbital radius of the electron in a hydrogen atom in the more physical model where reduced mass is included. This is done for convenience: the Bohr radius as defined above appears in equations relating to atoms other than hydrogen, where the reduced mass correction is different. If the definition of Bohr radius included the reduced mass of hydrogen, it would be necessary to include a more complex adjustment in equations relating to other atoms. The Bohr radius of the electron is one of a trio of related units of length, the other two being the Compton wavelength of the electron The Bohr radius including the effect of reduced mass can be given by the following equation:
where
In the above equation, the effect of the reduced mass is achieved by using the increased Compton wavelength, which is just the Compton wavelengths of the electron and the proton added together. |
||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Bohr_radius". A list of authors is available in Wikipedia. | ||||||||||||




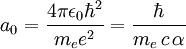
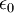 is the permittivity of free space
is the permittivity of free space
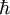 is the reduced Planck's constant
is the reduced Planck's constant
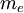 is the electron rest mass
is the electron rest mass
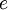 is the elementary charge
is the elementary charge
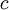 is the
is the 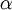 is the fine structure constant
is the fine structure constant
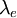 and the
and the 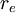 . The Bohr radius is built from the
. The Bohr radius is built from the 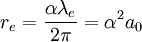
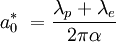 ,
,
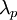 is the Compton wavelength of the
is the Compton wavelength of the 

