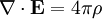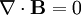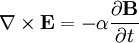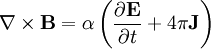To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Atomic unitsAtomic units (au) form a system of units convenient for atomic physics, electromagnetism, and quantum electrodynamics, especially when the focus is on the properties of electrons. There are two different kinds of atomic units, which one might name Hartree atomic units and Rydberg atomic units, which differ in the choice of the unit of mass and charge. This article deals with Hartree atomic units. In au, the numerical values of the following six physical constants are all unity by definition:
Product highlight
Fundamental units
These six quantities are not independent; to normalize all six quantities to 1, it suffices to normalize any four of them to 1. The normalizations of the Hartree energy and Coulomb's constant, for example, are only an incidental consequence of normalizing the other four quantities. Some derived units
Comparison with Planck unitsBoth Planck units and au are derived from certain fundamental properties of the physical world, and are free of anthropocentric considerations. To facilitate comparing the two systems of units, the above tables show the order of magnitude, in SI units, of the Planck unit corresponding to each atomic unit. Generally, when an atomic unit is "large" in SI terms, the corresponding Planck unit is "small", and vice versa. It should be kept in mind that au were designed for atomic-scale calculations in the present-day Universe, while Planck units are more suitable for quantum gravity and early-Universe cosmology. Both au and Planck units normalize the Dirac constant and the Coulomb force constant to 1. Beyond this, Planck units normalize to 1 the two fundamental constants of general relativity and cosmology: the gravitational constant G and the speed of light in a vacuum, c. Letting α denote the fine structure constant, the au value of c is α-1 ≈ 137.036. Atomic units, by contrast, normalize to 1 the mass and charge of the electron, and a0, the Bohr radius of the hydrogen atom. Normalizing a0 to 1 amounts to normalizing the Rydberg constant, R∞, to 4π/α = 4πc. Given au, the Bohr magneton μB=1/2. The corresponding Planck value is e/2me. Finally, au normalize a unit of atomic energy to 1, while Planck units normalize to 1 Boltzmann's constant k, which relates energy and temperature. Quantum mechanics and electrodynamics simplifiedThe (non-relativistic) Schrödinger equation for an electron in SI units is
The same equation in au is
For the special case of the electron around a hydrogen atom, the Hamiltonian in SI units is:
while atomic units transform the preceding equation into
Finally, Maxwell's equations take the following elegant form in au: (There is actually some ambiguity in defining the atomic unit of magnetic field. The above Maxwell equations use the "Gaussian" convention, in which a plane wave has electric and magnetic fields of equal magnitude. In the "Lorentz force" convention, a factor of α is absorbed into B.) See also
References
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Atomic_units". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





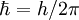
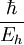
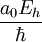
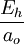
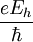
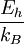
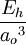
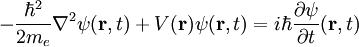 .
.
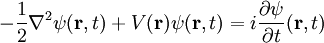 .
.
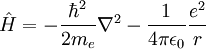 ,
,
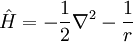 .
.