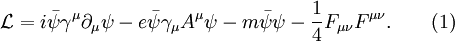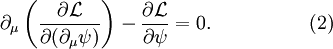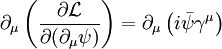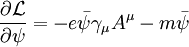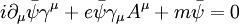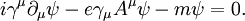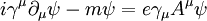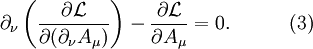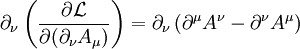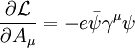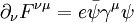To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Quantum electrodynamics
Quantum electrodynamics (QED) is a relativistic quantum field theory of electrodynamics. QED was developed by a number of physicists, beginning in the late 1920s.[1] QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons. It has been called "the jewel of physics" for its extremely accurate predictions of quantities like the anomalous magnetic moment of the electron, and the Lamb shift of the energy levels of hydrogen. Product highlight
HistoryThe word 'quantum' is Latin, meaning "how much" (neut. sing. of quantus "how great").[2] The word 'electrodynamics' was coined by André-Marie Ampère in 1822.[3] The word 'quantum', as used in physics, was first used by Max Planck, i.e. "energy elements", in 1900 and reinforced by Einstein in 1905 with his use of the term light quanta. Quantum theory began in 1900, when Max Planck assumed that energy is quantized in order to derive a formula predicting the observed frequency dependence of the energy emitted by a black body. This dependence is completely at variance with classical physics. In 1905, Einstein explained the photoelectric effect by postulating that light energy comes in quanta later called photons. In 1913, Bohr invoked quantization in his proposed explanation of the spectral lines of the hydrogen atom. In 1924, Louis de Broglie proposed a quantum theory of the wave-like nature of subatomic particles. The phrase "quantum physics" was first employed in Johnston's Planck's Universe in Light of Modern Physics. These theories, while they fit the experimental facts to some extent, were strictly phenomenological: they provided no rigorous justification for the quantization they employed. Modern quantum mechanics was born in 1925 with Werner Heisenberg's matrix mechanics and Erwin Schrödinger's wave mechanics and the Schrödinger equation, which was a non-relativistic generalization of de Broglie's(1925) relativistic approach. Schrödinger subsequently showed that these two approaches were equivalent. In 1927, Heisenberg formulated his uncertainty principle, and the Copenhagen interpretation of quantum mechanics began to take shape. Around this time, Paul Dirac, in work culminating in his 1930 monograph finally joined quantum mechanics and special relativity, pioneered the use of operator theory, and devised the bra-ket notation widely used since. In 1932, John von Neumann formulated the rigorous mathematical basis for quantum mechanics as the theory of linear operators on Hilbert spaces. This and other work from the founding period remains valid and widely used. Quantum chemistry began with Walter Heitler and Fritz London's 1927 quantum account of the covalent bond of the hydrogen molecule. Linus Pauling and others contributed to the subsequent development of quantum chemistry. The application of quantum mechanics to fields rather than single particles, resulting in what are known as quantum field theories, began in 1927. Early contributors included Dirac, Wolfgang Pauli, Weisskopf, and Jordan. This line of research culminated in the 1940s in the quantum electrodynamics (QED) of Richard Feynman, Freeman Dyson, Julian Schwinger, and Sin-Itiro Tomonaga, for which Feynman, Schwinger and Tomonaga received the 1965 Nobel Prize in Physics. QED, a quantum theory of electrons, positrons, and the electromagnetic field, was the first satisfactory quantum description of a physical field and of the creation and annihilation of quantum particles. QED involves a covariant and gauge invariant prescription for the calculation of observable quantities. Feynman's mathematical technique, based on his diagrams, initially seemed very different from the field-theoretic, operator-based approach of Schwinger and Tomonaga, but Freeman Dyson later showed that the two approaches were equivalent. The renormalization procedure for eliminating the awkward infinite predictions of quantum field theory was first implemented in QED. Even though renormalization works very well in practice, Feynman was never entirely comfortable with its mathematical validity, even referring to renormalization as a "shell game" and "hocus pocus". (Feynman, 1985: 128) QED has served as a role model and template for all subsequent quantum field theories. One such subsequent theory is quantum chromodynamics, which began in the early 1960s and attained its present form in the 1975 work by H. David Politzer, Sidney Coleman, David Gross and Frank Wilczek. Building on the pioneering work of Schwinger, Peter Higgs, Goldstone, and others, Sheldon Glashow, Steven Weinberg and Abdus Salam independently showed how the weak nuclear force and quantum electrodynamics could be merged into a single electroweak force. Physical interpretation of QEDIn classical optics light travels over all allowed paths, and their interference results in Fermat's principle. Similarly, in QED light (or any other particle like an electron or a proton) passes over every possible path allowed by apertures or lenses. The observer (at a particular location) simply detects the mathematical result of all wave functions added up, as a sum of all line integrals. For other interpretations, paths are viewed as non physical, mathematical constructs that are equivalent to other, possibly infinite, sets of mathematical expansions. According to QED, light can go slower or faster than c, but will travel at speed c on average[4]. Physically, QED describes charged particles (and their antiparticles) interacting with each other by the exchange of photons. The magnitude of these interactions can be computed using perturbation theory; these rather complex formulas have a remarkable pictorial representation as Feynman diagrams [1]. QED was the theory to which Feynman diagrams were first applied. These diagrams were invented on the basis of Lagrangian mechanics. Using a Feynman diagram, one decides every possible path between the start and end points. Each path is assigned a complex-valued probability amplitude, and the actual amplitude we observe is the sum of all amplitudes over all possible paths. Obviously, among all possible paths the ones with stationary phase contribute most (due to lack of destructive interference with some neighboring counter-phase paths) — this results in the stationary classical path between the two points. QED doesn't predict what will happen in an experiment, but it can predict the probability of what will happen in an experiment, which is how it is experimentally verified. Predictions of QED agree with experiments to an extremely high degree of accuracy: currently about 10−12 (and limited by experimental errors); for details see precision tests of QED. This makes QED the most accurate physical theory constructed thus far. Near the end of his life, Richard P. Feynman gave a series of lectures on QED intended for the lay public. These lectures were transcribed and published as Feynman (1985), QED: The strange theory of light and matter, a classic non-mathematical exposition of QED from the point of view articulated above.
MathematicsMathematically, QED has the structure of an abelian gauge theory, with the symmetry group U(1) as gauge group. The gauge field which mediates the interaction between the charged spin-1/2 fields is the electromagnetic field. The QED Lagrangian for the interaction of electrons and positrons through photons is
Euler-Lagrange equationsTo begin, plug in the definition of D into the Lagrangian to see that L is One can plug this Lagrangian into the Euler-Lagrange equation of motion for a field to find the field equations for QED. The two terms from this lagrangian are then Plugging these two back into the Euler-Lagrange equation (2) results in and the complex conjugate If you bring the middle term to the right-hand side looks like: The left hand side is like the original Dirac equation and the right hand side is the interaction with the electromagnetic field. One more important equation can be found by plugging in the lagrangian into one more Euler-lagrange equation, but now for the field, Aμ: The two terms this time are And these two terms, when plugged back into (3) give In picturesThe part of the Lagrangian containing the electromagnetic field tensor describes the free evolution of the electromagnetic field, whereas the Dirac-like equation with the gauge covariant derivative describes the free evolution of the electron and positron fields as well as their interaction with the electromagnetic field. See also
References
Further readingBooks
Journals
|
|||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Quantum_electrodynamics". A list of authors is available in Wikipedia. |





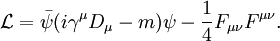
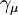 are Dirac matrices.
are Dirac matrices.
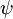 and its Dirac adjoint
and its Dirac adjoint 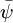 are the fields representing
are the fields representing 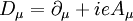 is the gauge covariant derivative, with
is the gauge covariant derivative, with 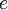 the coupling strength (equal to the elementary charge),
the coupling strength (equal to the elementary charge),
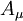 the covariant vector potential of the electromagnetic field and
the covariant vector potential of the electromagnetic field and
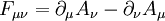 the electromagnetic field tensor.
the electromagnetic field tensor.