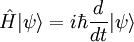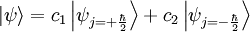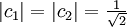To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Stern–Gerlach experiment
In quantum mechanics, the Stern–Gerlach experiment, named after Otto Stern and Walther Gerlach, is a celebrated experiment (performed in 1922) on the deflection of particles, often used to illustrate basic principles of quantum mechanics. It can be used to demonstrate that electrons and atoms have intrinsically quantum properties, and how measurement in quantum mechanics affects the system being measured. Product highlight
Basic theory and descriptionOtto Stern and Walther Gerlach devised an experiment to determine whether particles had any intrinsic angular momentum. In a classical system, such as the earth orbiting the sun, the earth has angular momentum from both its orbit around the sun and the orbit around its axis (its spin). The experiment sought to determine whether individual particles like electrons have any "spin" angular momentum.[dubious] If the electron is treated like a classical dipole with two halves of charge spinning quickly, it will begin to precess in a magnetic field, because of the torque that the magnetic field exerts on the dipole (see Torque-induced precession). If the particle travels in a homogeneous magnetic field, the forces exerted on opposite ends of the dipole cancel each other out and the motion of the particle is unaffected. If the experiment is conducted using electrons, an electric field of appropriate magnitude and oriented transverse to the charged particle's path is used to compensate for the tendency of any charged particle to curl in its path through a magnetic field (see cyclotron motion), and the fact that electrons are charged can safely be ignored. The Stern–Gerlach experiment can be conducted using electrically neutral particles and the same conclusion is reached, since it is designed to test angular momentum only, not any electrostatic phenomena. If the particle travels through an inhomogeneous magnetic field, then the force on one end of the dipole will be slightly greater than the opposing force on the other end of the dipole. This leads to the particle being deflected in the inhomogeneous magnetic field. The direction in which the particles are deflected is typically called the "z" direction. If the particles are classical, "spinning" particles, then the distribution of their spin angular momentum vectors is taken to be truly random and each particle would be deflected up or down by a different amount, producing an even distribution on the screen of a detector. Instead, the particles passing through the device are deflected either up or down by a specific amount. This can only mean that spin angular momentum is quantized, i.e. it can only take on discrete values. There is not a continuous distribution of possible angular momenta. Electrons are spin-½ particles. These have only two possible spin values, called spin-up and spin-down. The exact value of their spin is +ħ/2 or -ħ/2. If this value arises as a result of the particles rotating the way a planet rotates, then the individual particles would have to be spinning impossibly fast. The speed of rotation would be in excess of the speed of light and thus impossible.[1] Thus, the spin angular momentum has nothing to do with rotation and is a purely quantum mechanical phenomenon. That is why it is sometimes known as the "intrinsic angular momentum." For electrons, two possible values for spin exist, as well as for the proton and the neutron, which are composite particles made up of three quarks each, which are themselves spin-½ particles. Other particles may have a different number of possible values. Delta baryons (Δ++, Δ+, Δ0, Δ−), for example, are spin-3/2 particles and have four possible values for spin angular momentum. Vector mesons, as well as photons, W and Z bosons and gluons are spin-1 particles and have three possible values for spin angular momentum. To describe the experiment with spin-½ particles mathematically, it is easiest to use Dirac's bra-ket notation. As the particles pass through the Stern-Gerlach device, they are "being observed." The act of observation in quantum mechanics is equivalent to measuring them. Our observation device is the detector and in this case we can observe one of two possible values, either spin up or spin down. These are described by the angular momentum quantum number j, which can take on one of the two possible allowed values, either +ħ/2 or -ħ/2. The act of observing (measuring) corresponds to the operator Jz. In mathematical terms, The constants c1 and c2 are complex numbers. The square of their absolute values determines the probability of the state |ψ> being found with one of the two possible values for j. The constants must also be normalized so the probability of finding the wavefunction in one of either state is unity. Here we know that the probability of finding the particle in each state is 0.5. However, this information is not sufficient to determine the values of c1 and c2, because they may in fact be complex numbers. Therefore we only know the absolute values of the constants. These are Sequential experimentsIf we combine some Stern–Gerlach apparati we can clearly see that they do not act as simple selectors, but alter the states observed (as in light polarization), according to quantum mechanics laws: HistoryThe Stern–Gerlach experiment was performed in Frankfurt, Germany in 1922 by Otto Stern and Walther Gerlach. At the time, Stern was an assistant to Max Born at the University of Frankfurt's Institute for Theoretical Physics, and Gerlach was an assistant at the same university's Institute for Experimental Physics. At the time of the experiment, the most prevalent model for describing the atom was the Bohr model, which described electrons as going around the positively-charged nucleus only in certain discrete atomic orbitals or energy levels. Since the electron was quantized to be only in certain positions in space, the separation into distinct orbits was referred to as space quantization. ImpactThe Stern–Gerlach experiment had one of the biggest impacts on modern physics:
See also
References
|
|||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Stern–Gerlach_experiment". A list of authors is available in Wikipedia. |