To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Wave–particle duality
In physics and chemistry, wave–particle duality is the concept that all matter exhibits both wave-like and particle-like properties. A central concept of quantum mechanics, duality addresses the inadequacy of classical concepts like "particle" and "wave" in fully describing the behaviour of objects. Various interpretations of quantum mechanics attempt to explain this ostensible paradox. The idea of duality is rooted in a debate over the nature of light and matter dating back to the 1600s, when competing theories of light were proposed by Christiaan Huygens and Isaac Newton. Through the work of Albert Einstein, Louis de Broglie and many others, current scientific theory holds that all particles also have a wave nature.[1] This phenomenon has been verified not only for elementary particles, but also for compound particles like atoms and even molecules. In fact, according to traditional formulations of non-relativistic quantum mechanics, wave–particle duality applies to all objects, even macroscopic ones; we can't detect wave properties of macroscopic objects due to their small wavelengths.[2] Product highlight
Brief historyAt the close of the 19th century, the case for atomic theory, that matter was made of particulate objects or atoms, was well established. Electricity, first thought to be a fluid, was now understood to consist of particles called electrons, as demonstrated by J.J. Thomson who, led by his research into the work of Ernest Rutherford, had discovered using cathode rays that an electrical charge would actually travel across a vacuum from cathode to anode. In brief, it was understood that much of nature was made of particles. At the same time, waves were well understood, together with wave phenomena such as diffraction and interference. Light was believed to be a wave, as Thomas Young's double-slit experiment and effects such as Fraunhofer diffraction had clearly demonstrated the wave-like nature of light. But as the 20th century turned, problems had emerged. Albert Einstein's analysis of the photoelectric effect in 1905 demonstrated that light also possessed particle-like properties, and this was further confirmed with the discovery of the Compton effect in 1923. Later on, the diffraction of electrons would be predicted and experimentally confirmed, thus showing that electrons must have wave-like properties in addition to particle properties. This confusion over particle versus wave properties was eventually resolved with the advent and establishment of quantum mechanics in the first half of the 20th century, which ultimately explained wave–particle duality. It provided a single unified theoretical framework for understanding that all matter may have characteristics associated with particles and waves, as explained below. By the very end of the 20th century extremely precise results were obtained quantifying this duality, in the form of the Englert-Greenberger duality relation. Developmental milestonesHuygens and NewtonThe earliest comprehensive theory of light was advanced by Christiaan Huygens, who proposed a wave theory of light, and in particular demonstrated how waves might interfere to form a wavefront, propagating in a straight line. However, the theory had difficulties in other matters, and was soon overshadowed by Isaac Newton's corpuscular theory of light. That is, Newton proposed that light consisted of small particles, with which he could easily explain the phenomenon of reflection. With considerably more difficulty, he could also explain refraction through a lens, and the splitting of sunlight into a rainbow by a prism. Newton's particle viewpoint went essentially unchallenged for over a century.[3] Young, Fresnel, and MaxwellIn the early 1800s, the double-slit experiments by Young and Fresnel provided evidence for Huygens' wave theories: these experiments showed that when light is sent through a grid, a characteristic interference pattern is observed, very similar to the pattern resulting from the interference of water waves; the wavelength of light can be computed from such patterns. The wave view did not immediately displace the ray and particle view, but began to dominate scientific thinking about light in the mid 1800s, since it could explain polarization phenomena that the alternatives could not. Maxwell, during the late 1800s, explained light as the propagation of electromagnetic waves with the Maxwell equations. These equations were verified by experiment, and Huygens' view became widely accepted. Planck's formula for black body radiationIn 1901, Max Planck published an analysis that succeeded in reproducing the observed spectrum of light emitted by a glowing object. To accomplish this, Planck had to make an ad hoc mathematical assumption of quantized energy of the oscillators (atoms of the blackbody) that emit radiation. It was Einstein who later proposed that it is the electromagnetic radiation itself that is quantized, and not the energy of radiating atoms. Einstein's explanation of the photoelectric effect
In 1905, Albert Einstein provided an explanation of the photoelectric effect, a hitherto troubling experiment that the wave theory of light seemed incapable of explaining. He did so by postulating the existence of photons, quanta of light energy with particulate qualities. In the photoelectric effect, it was observed that shining a light on certain metals would lead to an electric current in a circuit. Presumably, the light was knocking electrons out of the metal, causing current to flow. However, it was also observed that while a dim blue light was enough to cause a current, even the strongest, brightest red light caused no current at all. According to wave theory, the strength or amplitude of a light wave was in proportion to its brightness: a bright light should have been easily strong enough to create a large current. Yet, oddly, this was not so. Einstein explained this conundrum by postulating that the electrons can receive energy from electromagnetic field only in discrete portions (quanta that were called photons): an amount of energy E that was related to the frequency, f of the light by where h is Planck's constant (6.626 × 10-34 J seconds). Only photons of a high-enough frequency, (above a certain threshold value) could knock an electron free. For example, photons of blue light had sufficient energy to free an electron from the metal, but photons of red light did not. More intense light above the threshold frequency could release more electrons, but no amount of light below the threshold frequency could release an electron. Einstein was awarded the Nobel Prize in Physics in 1921 for his theory of the photoelectric effect. de Broglie's hypothesisIn 1924, Louis-Victor de Broglie formulated the de Broglie hypothesis, claiming that all matter,[4][5] not just light, has a wave-like nature; he related wavelength (denoted as λ), and momentum (denoted as p): This is a generalization of Einstein's equation above, since the momentum of a photon is given by p=E/c and the wavelength by λ=c/f, where c is the speed of light in vacuum. De Broglie's formula was confirmed three years later for electrons (which differ from photons in having a rest mass) with the observation of electron diffraction in two independent experiments. At the University of Aberdeen, George Paget Thomson passed a beam of electrons through a thin metal film and observed the predicted interference patterns. At Bell Labs Clinton Joseph Davisson and Lester Halbert Germer guided their beam through a crystalline grid. De Broglie was awarded the Nobel Prize for Physics in 1929 for his hypothesis. Thomson and Davisson shared the Nobel Prize for Physics in 1937 for their experimental work. Heisenberg's uncertainty principleIn his work on formulating quantum mechanics, Werner Heisenberg postulated his uncertainty principle, which states: where
Heisenberg originally explained this as a consequence of the process of measuring: Measuring position accurately would disturb momentum and vice-versa, offering an example (the "gamma-ray microscope") that depended crucially on the de Broglie hypothesis. It is now understood, however, that this only partly explains the phenomenon: the uncertainty also exists in the particle itself, even before the measurement is made. In fact, the modern explanation of the uncertainty principle, extending the Copenhagen interpretation first put forward by Bohr and Heisenberg, depends even more centrally on the wave nature of a particle: Just as it is nonsensical to discuss the precise location of a wave on a string, particles do not have perfectly precise positions; likewise, just as it is nonsensical to discuss the wavelength of a "pulse" wave traveling down a string, particles do not have perfectly precise momenta (which corresponds to the inverse of wavelength). Moreover, when position is relatively well defined, the wave is pulse-like and has a very ill-defined wavelength (and thus momentum). And conversely, when momentum (and thus wavelength) is relatively well defined, the wave looks long and sinusoidal, and therefore it has a very ill-defined position. De Broglie himself had proposed a pilot wave construct to explain the observed wave–particle duality. In this view, each particle has a well-defined position and momentum, but is guided by a wave function derived from Schrödinger's equation. The pilot wave theory was initially rejected because it generated non-local effects when applied to systems involving more than one particle. Non-locality, however, soon became established as an integral feature of quantum theory (see EPR paradox), and David Bohm extended de Broglie's model to explicitly include it. In Bohmian mechanics,[6] the wave–particle duality is not a property of matter itself, but an appearance generated by the particle's motion subject to a guiding equation or quantum potential. Wave behavior of large objectsSince the demonstrations of wave-like properties in photons and electrons, similar experiments have been conducted with neutrons and protons. Among the most famous experiments are those of Estermann and Otto Stern in 1929.[citation needed] Authors of similar recent experiments with atoms and molecules, described below, claim that these larger particles also act like waves. A dramatic series of experiments emphasizing the action of gravity in relation to wave–particle duality were conducted in the 1970s using the neutron interferometer.[citation needed] Neutrons, one of the components of the atomic nucleus, provide much of the mass of a nucleus and thus of ordinary matter. In the neutron interferometer, they act as quantum-mechanical waves directly subject to the force of gravity. While the results were not surprising since gravity was known to act on everything, including light (see tests of general relativity and the Pound-Rebka falling photon experiment), the self-interference of the quantum mechanical wave of a massive fermion in a gravitational field had never been experimentally confirmed before. In 1999, the diffraction of C60 fullerenes by researchers from the University of Vienna was reported.[7] Fullerenes are comparatively large and massive objects, having an atomic mass of about 720 u. The de Broglie wavelength is 2.5 pm, whereas the diameter of the molecule is about 1 nm, i.e. about 400 times larger. As of 2005, this is the largest object for which quantum-mechanical wave-like properties have been directly observed in far-field diffraction. In 2003 the Vienna group also demonstrated the wave nature of tetraphenylporphyrin[8] – a flat biodye with an extension of about 2 nm and a mass of 614 u. For this demonstration they employed a near-field Talbot Lau interferometer.[9][10] In the same interferometer they also found interference fringes for C60F48., a fluorinated buckyball with a mass of about 1600 u, composed of 108 atoms[8] Large molecules are already so complex that they give experimental access to some aspects of the quantum-classical interface, i.e. to certain decoherence mechanisms.[11][12] Whether objects heavier than the Planck mass (about the weight of a large bacterium) have a de Broglie wavelength is theoretically unclear and experimentally unreachable; above the Planck mass a particle's Compton wavelength would be smaller than the Planck length and its own Schwarzschild radius, a scale at which current theories of physics may break down or need to be replaced by more general ones.[13] Treatment in modern quantum mechanicsWave–particle duality is deeply embedded into the foundations of quantum mechanics, so well that modern practitioners rarely discuss it as such. In the formalism of the theory, all the information about a particle is encoded in its wave function, a complex function roughly analogous to the height of a wave at each point in space. This function evolves according to a differential equation (generically called the Schrödinger equation), and this equation gives rise to wave-like phenomena such as interference and diffraction. The particle-like behavior is most evident due to phenomena associated with measurement in quantum mechanics. Upon measuring the location of the particle, the wave-function will randomly "collapse" to a sharply peaked function at some location, with the likelihood of any particular location equal to the squared amplitude of the wave-function there. The measurement will return a well-defined position, a property traditionally associated with particles. Although this picture is somewhat simplified (to the non-relativistic case), it is adequate to capture the essence of current thinking on the phenomena historically called "wave–particle duality". (See also: Mathematical formulation of quantum mechanics.) Alternative viewsParticle-only viewAt least one physicist considers the “wave-duality” a misnomer, as L. Ballentine, Quantum Mechanics, A Modern Development, p.4, explains: When first discovered, particle diffraction was a source of great puzzlement. Are “particles” really “waves? in the early experiments, the diffraction patterns were detected holistically by means of a photographic plate, which could not detect individual particles. As a result, the notion grew that particle and wave properties were mutually incompatible, or complementary, in the sense that different measurement apparatuses would be required to observe them. That idea, however, was only an unfortunate generalization from a technological limitation. Today it is possible to detect the arrival of individual electrons, and to see the diffraction pattern emerge as a statistical pattern made up of many small spots (Tonomura et al., 1989). Evidently, quantum particles are indeed particles, but whose behaviour is very different from classical physics would have us to expect. Prominent physicist Richard Feynman wrote:[14] I want to emphasize that light comes in this form—particles. It is very important to know that light behaves like particles, especially for those of you who have gone to school, where you were probably told something about light behaving like waves. I'm telling you the way it does behave—like particles. Wave-only viewAt least one scientist proposes that the duality can be replaced by a "wave-only" view. Carver Mead's Collective Electrodynamics: Quantum Foundations of Electromagnetism (2000) analyzes the behavior of electrons and photons purely in terms of electronic wave functions, and attributes the apparent particle-like behavior to quantization effects and eigenstates. According to reviewer David Haddon:[15] Mead has cut the Gordian knot of quantum complementarity. He claims that atoms, with their neutrons, protons, and electrons, are not particles at all but pure waves of matter. Mead cites as the gross evidence of the exclusively wave nature of both light and matter the discovery between 1933 and 1996 of ten examples of pure wave phenomena, including the ubiquitous laser of CD players, the self-propagating electrical currents of superconductors, and the Bose–Einstein condensate of atoms. ApplicationsAlthough it is difficult to draw a line separating wave–particle duality from the rest of quantum mechanics, it is nevertheless possible to list some applications of this basic idea.
See also
References
|
|||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Wave–particle_duality". A list of authors is available in Wikipedia. |


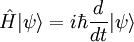



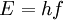
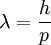
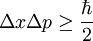
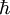 is the reduced Planck's constant (Planck's constant divided by 2
is the reduced Planck's constant (Planck's constant divided by 2

