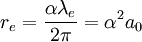To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Compton wavelength
The Compton wavelength
Product highlightwhere
The CODATA 2002 value for the Compton wavelength of the electron is 2.4263102175×10-12 meter with a standard uncertainty of 0.0000000033×10-12 m.[1] Other particles have different Compton wavelengths. The Compton wavelength can be thought of as a fundamental limitation on measuring the position of a particle, taking quantum mechanics and special relativity into account.
This depends on the mass This argument also shows that the Compton wavelength is the cutoff below which quantum field theory– which can describe particle creation and annihilation – becomes important. We can make the above argument a bit more precise as follows. Suppose we wish to measure the position of a particle to within an accuracy
so the uncertainty in the particle's momentum satisfies
Using the relativistic relation between momentum and energy,
when Δp exceeds mc then the uncertainty in energy is greater than
So, at least to within an order of magnitude, the uncertainty in
position must be greater than the Compton wavelength The Compton wavelength can be contrasted with the de Broglie wavelength, which depends on the momentum of a particle and determines the cutoff between particle and wave behavior in quantum mechanics. For fermions, the Compton wavelength sets the cross-section of interactions. For example, the cross-section for Thomson scattering of a photon from an electron is equal to
where The Compton wavelength of the electron is one of a trio of related units of length, the other two being the Bohr radius a0 and the classical electron radius re. The Compton wavelength is built from the electron mass me, Planck's constant h and the speed of light c. The Bohr radius is built from me, h and the electron charge e. The classical electron radius is built from me, c and e. Any one of these three lengths can be written in terms of any other using the fine structure constant α:
References
Categories: Atomic physics | Foundational quantum physics |
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Compton_wavelength". A list of authors is available in Wikipedia. |


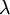 of a particle is given by
of a particle is given by
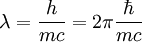 ,
,



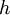 is the Planck constant,
is the Planck constant,
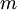 is the particle's mass,
is the particle's mass,
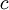 is the
is the 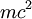 , when one hits the particle whose position is being measured the collision may have enough energy to create a new particle of the same type. This
renders moot the question of the original particle's location.
, when one hits the particle whose position is being measured the collision may have enough energy to create a new particle of the same type. This
renders moot the question of the original particle's location.
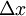 .
Then the uncertainty relation for position and
.
Then the uncertainty relation for position and 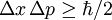
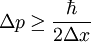
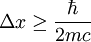
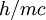 .
.
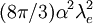 ,
,
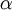 is the fine-structure constant and
is the fine-structure constant and 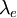 is the Compton wavelength of the electron. For gauge
is the Compton wavelength of the electron. For gauge