Classical electron radius

The classical electron radius, also known as the Compton radius or the Thomson scattering length is based on a classical (i.e., non-quantum) relativistic model of the electron. Its value is calculated as

Additional recommended knowledge

Daily Visual Balance Check

Correct Test Weight Handling Guide: 12 Practical Tips

Daily Sensitivity Test

where e and m are the electric charge and the mass of the electron, c is the speed of light, and ε₀ is the permittivity of free space.

Using classical electrostatics, the energy required to assemble a sphere of constant charge density, of radius r_e and charge e is

.

If the charge is on the surface the energy is

.

Ignoring the factors 3/5 or 1/2, if this is equated to the relativistic energy of the electron (E = mc²) and solved for r_e, the above result is obtained.

In simple terms, the classical electron radius is roughly the size the electron would need to have for its mass to be completely due to its electrostatic potential energy - not taking quantum mechanics into account. We now know that quantum mechanics, indeed quantum field theory, is needed to understand the behavior of electrons at such short distance scales, thus the classical electron radius is no longer regarded as the actual size of an electron. In fact, modern particle physics experiments indicate that the electron is a point particle, i.e. it has no size and its radius is zero. Still, the classical electron radius is used in modern classical-limit theories involving the electron, such as non-relativistic Thomson scattering and the relativistic Klein-Nishina formula. Also, the classical electron radius is roughly the length scale at which renormalization becomes important in quantum electrodynamics.

The classical electron radius is one of a trio of related units of length, the other two being the Bohr radius a₀ and the Compton wavelength of the electron λ_e. The classical electron radius is built from the electron mass m_e, the speed of light c and the electron charge e. The Bohr radius is built from m_e, e and Planck's constant h. The Compton wavelength is built from m_e, h and c. Any one of these three lengths can be written in terms of any other using the fine structure constant α:

Extrapolating from the initial equation, any mass m₀ can be imagined to have an 'electromagnetic radius' similar to the electron's classical radius.

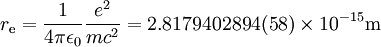
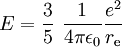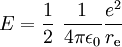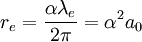
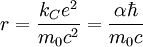
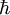where k_C is Coulomb's constant, α is the fine structure constant and is Planck's constant. Such a radius does not exist as a physical entity but it is sometimes useful in theoretical calculations.

References

• CODATA value for the classical electron radius at NIST.
• Arthur N. Cox, Ed. "Allen's Astrophysical Quantities", 4th Ed, Springer, 1999.