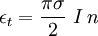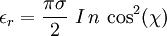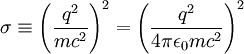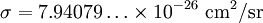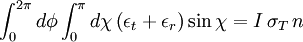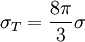My watch list

Thomson scattering

In physics, Thomson scattering is the scattering of electromagnetic radiation by a charged particle. The electric and magnetic components of the incident wave accelerate the particle. As it accelerates, it in turn emits radiation and thus, the wave is scattered. Thomson scattering is an important phenomenon in plasma physics and was first explained by the physicist J.J. Thomson.

Additional recommended knowledge

Daily Sensitivity Test

What is the Sensitivity of my Balance?

Correct Test Weight Handling Guide: 12 Practical Tips

As long as the motion of the particle is non-relativistic (i.e. its speed is much less than the speed of light), the main cause of the acceleration of the particle will be due to the electric field component of the incident wave. The particle will move in the direction of the oscillating electric field, resulting in electromagnetic dipole radiation. The moving particle radiates most strongly in a direction perpendicular to its motion and that radiation will be polarized along the direction of its motion. Therefore, depending on where an observer is located, the light scattered from a small volume element may appear to be more or less polarized.

The electric fields of the incoming and observed beam can be divided up into those components lying in the plane of observation (formed by the incoming and observed beams) and those components perpendicular to that plane. Those components lying in the plane are referred to as "radial" and those perpendicular to the plane are "tangential", since this is how they appear to the observer.

The diagram on the right is in the plane of observation. It shows the radial component of the incident electric field causing a component of motion of the charged particles at the scattering point which also lies in the plane of observation. It can be seen that the amplitude of the wave observed will be proportional to the cosine of χ, the angle between the incident and observed beam. The intensity, which is the square of the amplitude, will then be diminished by a factor of cos²(χ). It can be seen that the tangential components (perpendicular to the plane of the diagram) will not be affected in this way.

The scattering is best described by an emission coefficient which is defined as ε where ε dt dV dΩ dλ is the energy scattered by a volume element $d V$ in time dt into solid angle dΩ between wavelengths λ and λ+dλ. From the point of view of an observer, there are two emission coefficients, ε_r corresponding to radially polarized light and ε_t corresponding to tangentially polarized light. For unpolarized incident light, these are given by:

$\epsilon_t = \frac{\pi \sigma }{2}~I\,n$

$\epsilon_r = \frac{\pi \sigma }{2}~I\,n\,\cos^2(\chi)$

where n is the density of charged particles at the scattering point, I is incident flux (e.g. energy/time/area/wavelength) and σ is the Thomson differential cross section for the charged particles (area/solid angle), which is

$\sigma \equiv \left(\frac{q^2}{mc^2}\right)^2=\left(\frac{q^2}{4\pi\epsilon_0mc^2}\right)^2$

where the first expression is in cgs units, the second in SI units; q is the charge per particle, m the mass per particle, and $ε 0$ a constant, the permittivity of free space.

Note that this is the square of the classical radius of a point particle of mass m and charge q. For example, for an electron, the differential cross section is:

$\sigma =7.94079\ldots\times 10^{-26}~\textrm{cm}^2/\textrm{sr}$

The total energy radiated is found by integrating the sum of the emission coefficients over all directions:

$\int_0^{2\pi}d\phi \int_0^\pi d\chi \left(\epsilon_t+\epsilon_r\right) \sin \chi = I\,\sigma_T\,n$

where σ_T is the total cross section:

$\sigma_T = \frac{8\pi}{3}\sigma$

which for an electron has a value of 6.652...× 10⁻²⁵ cm².

Examples of Thomson scattering

The cosmic microwave background is thought to be linearly polarized as a result of Thomson scattering. Probes such as WMAP and the future Planck mission attempt to measure this polarization.

The solar K-corona is the result of the Thomson scattering of solar radiation from solar coronal electrons. NASA's STEREO mission will generate three-dimensional images of the electron density around the sun by measuring this K-corona from two separate satellites.

In tokamaks and other experimental fusion devices, the electron temperatures and densities in the plasma can be measured with high accuracy by detecting the effect of Thomson scattering of a high-intensity laser beam.

References

Billings, Donald E., ``A Guide to the Solar Corona, Academic Press, New York 1966.

Categories: Atomic physics | Scattering | Plasma physics

This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Thomson_scattering". A list of authors is available in Wikipedia.