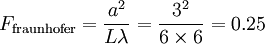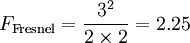To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Fraunhofer diffractionIn optics, Fraunhofer diffraction is a form of wave diffraction, which occurs when field waves are passed through an aperture or slit, causing only the size of an observed aperture image to change[1][2]due to the far-field location of observation and the increasingly planar nature of outgoing diffracted waves passing through the aperture. It is observed at distances beyond the near-field distance of Fresnel diffraction, which affects both the size and shape of the observed aperture image, and occurs only when the Fresnel number Product highlight
FormsExplanation
Fraunhofer diffraction goes from the idea of a wave being split into several outgoing waves when passed through an aperture, slit or hole, and is usually described through the use of observational experiments using lenses to purposefully diffract light. When waves pass through, the wave is split into two diffracted waves travelling at parallel angles to each other along with the continuing incoming wave, and are often used in methods of observation by placing a screen in its path in order to view the image-pattern observed.[3] When a diffracted wave is observed parallel to the other at an initial near-field distance, Fresnel diffraction is seen to occur due to the distance between the aperture and the observed canvas (σ) being more than 1 when calculated with the Fresnel number equation,[3] which can be used to observe the extent of diffraction in the parallel waves through the calculation of the aperture or slit size (a), wavelength (λ) and distance from the aperture, (L). When the distance or wavelength is increased,[2] Fraunhofer diffraction occurs due to the waves going towards becoming planar, over the extent of diffracting apertures or objects.[4] Aperture formWhen observed, the image of the aperture from Fresnel diffraction will change in terms of size and shape, namely, the edges become more or less "jagged", whereas the aperture image observed when Fraunhofer diffraction is in effect only alters in terms of size due to the more collimated or planar nature of the waves. The far-field diffraction pattern of a source may also be observed (except for scale) in the focal plane of a well-corrected lens. The far-field pattern of a diffracting screen illuminated by a point source may be observed in the image plane of the source. If a light source and an observation screen are effectively far enough from a diffraction aperture (for example a slit), then the wavefronts arriving at the aperture and the screen can be considered to be collimated, or plane. Fresnel diffraction, or near-field diffraction occurs when this is not the case and the curvature of the incident wavefronts is taken into account. In far-field diffraction, if the observation screen is moved relative to the aperture, the diffraction pattern produced changes uniformly in size. This is not the case in near-field diffraction, where the diffraction pattern changes both in size and shape. Slit formFraunhofer diffraction through a slit can be achieved with two lenses and a screen. Using a point-like source for light and a collimating lens it is possible to make parallel light, which will then be passed through the slit. After the slit there is another lens that will focus the parallel light onto a screen for observation. The same setup with multiple slits can also be used, creating a different diffraction pattern. Since this type of diffraction is mathematically simple, this experimental setup can be used to find the wavelength of the incident monochromatic light with high accuracy. Amplitude transmittanceIn this description, we assume that an incident electric or other field is described by
In what follows, all fields are assumed to have a time-dependence exp( − iωt). If this field is incident on an aperture in the xy-plane with a complex transmittance T(x,y), then the diffracted far-zone field as a function of the far field spherical coordinate system angles (θ,φ,r) can be calculated via the Huygens-Fresnel principle, using the parallel rays approximation, where k = 2π / λ is the circular wavenumber of the incident waves. The expression is the Fourier transform of the aperture function, with the Fourier kernel
Note that the aperture function acts on the complex field, not on the intensity (amplitude squared) of the waves. It can be complex-valued to indicate a phase shift. In many cases, there is no dependence on y and φ, and where we ignore the dependency on r as well. This is the Fourier transform from space coordinates x to In either approximation, the equation does not provide absolute amplitudes, since (electric) field integrated over spatial dimensions does not represent a conserved physical quantity such as energy or power. To obtain absolute amplitudes, normalization is necessary such that ExamplesSlit diffractionThe simplest example is Fraunhofer diffraction from a slit, i.e. f(x) = 1 for − a / 2 < x < a / 2 and f(x) = 0 elsewhere. In this case,
The unnormalized sinc function peaks at θ = 0 and has zeroes at Gaussian profileAn aperture with a Gaussian profile (for example a fuzzy transparent disc on a photographic slide) f(x) = exp( − ax2) results in For example, if a laser beam has an intensity profile with a full width at half maximum (FWHM) W, then a = 2ln2 / W2. At a wavelength λ, the amplitude profile is i.e. an angular FWHM in the intensity of ReferencesNotes
Book references
See also
|
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Fraunhofer_diffraction". A list of authors is available in Wikipedia. |


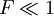 , wherein the parallel rays approximation can be applied.
, wherein the parallel rays approximation can be applied.



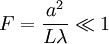
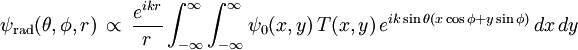
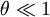 . The above integral can then be approximated as
. The above integral can then be approximated as
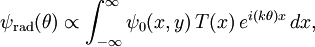
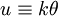 .
.
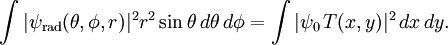
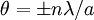 , where
, where 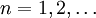 .
.
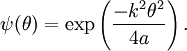
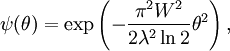
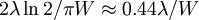 .
.