To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Fresnel diffraction
In optics, Fresnel diffraction or near-field diffraction is a process of diffraction which occurs when a wave passes through an aperture and diffracts in the near field, causing any diffraction pattern observed to differ in size and shape, relative to the distance. It occurs due to the short distance in which the diffracted waves propagate, which results in a fresnel number greater than 1 ( Product highlight
The Fresnel diffraction integralThe electric field diffraction pattern at a point (x,y,z) is given by: where
and
Analytical solution of this integral is impossible for all but the simplest diffraction geometries. Therefore, it is usually calculated numerically. The Fresnel approximationThe main problem for solving the integral is the expression of r. First, we can simplify the algebra by introducing the substitution: Substituting into the expression for r, we find: Next, using the Taylor series expansion we can express r as If we consider all the terms of Taylor series there is no approximation.[1]. Let us substitute this expression in the argument of the exponential within the integral; the key to the Fresnel approximation is to assume that the third element is very small and can be ignored. In order to make this possible, it has to contribute to the variation of the exponential for an almost null term. In other words, it has to be much smaller than the period of the complex exponential, i.e. 2π: expressing k in terms of the wavelength, we get the following relationship: Multiplying both sides by z / λ, we have or, substituting the earlier expression for ρ2 , If this condition holds true for all values of x, x' , y and y' , then we can ignore the third term in the Taylor expression. Furthermore, if the third term is negligible, then all terms of higher order will be even smaller, so we can ignore them as well. We can then approximate the expression with only the first two terms: This equation, then, is the Fresnel approximation, and the inequality stated above is a condition for the approximation's validity. Fresnel DiffractionThe condition for validity is fairly weak, and it allows all length parameters to take comparable values, provided the aperture is small compared to the path length. Moreover, if we are interested in the behaviour of the field only in a small area close to the origin, i.e. for values of x and y much smaller than z, then we can assume Unlike Fraunhofer diffraction, Fresnel diffraction has to account for the curvature of the wavefront, in order to correctly calculate the relative phase of interfering waves. For Fresnel diffraction the electric field at point (x,y,z) is given by: This is the Fresnel diffraction integral; it means that, if the Fresnel approximation is valid, the propagating field is a spherical wave, originating at the aperture and moving along z. The integral modulates the amplitude and phase of the spherical wave. Analytical solution of this expression is still only possible in rare cases. For a further simplified case, valid only for much larger distances from the diffraction source see Fraunhofer diffraction. Alternative formsConvolutionThe integral can be expressed in other ways in order to calculate it using some mathematical properties. If we define the following function: then the integral can be expressed in terms of a convolution: it other words we are representing the propagation using a linear-filter modeling. That is why we might call the function h(x,y) the impulse response of free space propagation. Fourier TransformAnother possible way is through the Fourier transform. If in the integral we express k in terms of the wavelength, and we expand each component of the transverse displacement, then we can express the integral in terms of the two dimensional Fourier transform. Let us use the following definition: where p and q are spatial frequencies (in units of lines/meter). The Fresnel integral can be expressed as: where
See also
Notes
[2] H. Oberst, D. Kouznetsov, K. Shimizu, J. Fujita, F. Shimizu. Fresnel diffraction mirror for atomic wave, Physical Review Letters, 94, 013203 (2005). References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Fresnel_diffraction". A list of authors is available in Wikipedia. |


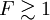 ). When the distance is increased, outgoing diffracted waves become planar and
). When the distance is increased, outgoing diffracted waves become planar and 


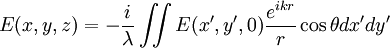
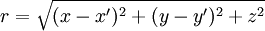
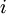 is the imaginary unit,
is the imaginary unit,
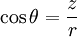 is the cosine of the angle between z and r.
is the cosine of the angle between z and r.
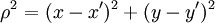
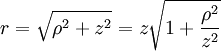
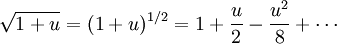
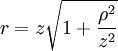
![= z \left[ 1 + \frac{\rho^2}{2 z^2} - \frac{1}{8} \left( \frac{\rho^2}{z^2} \right)^2 + \cdots \right]](images/math/4/7/4/47408fa98a6d8dae9ac96b5f82dcec14.png)
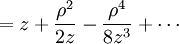
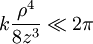
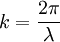
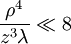
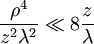
![\frac{[(x-x')^2+(y-y')^2]^2}{z^2 \lambda^2} \ll 8 {z \over \lambda}](images/math/6/9/d/69dc6acc6acf4da77acf1dd414955d06.png)
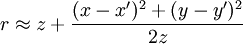
 , that means
, that means 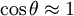 and the r in the denominator of the Fresnel integral can be approximated by
and the r in the denominator of the Fresnel integral can be approximated by 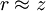 .
.
![E(x,y,z)=-{i \over \lambda}{e^{ikz} \over z}\iint E(x',y',0)e^{{ik \over 2z}[(x-x')^2+(y-y')^2]}dx'dy'](images/math/9/e/4/9e4c442405da7991234f337e7cbcb9a0.png)
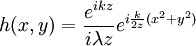
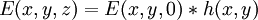
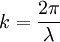
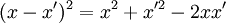
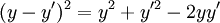
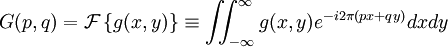
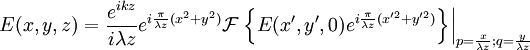
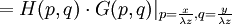
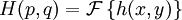
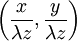 and multiply it for another factor. This expression is better than the others when the process leads to a known Fourier transform.
and multiply it for another factor. This expression is better than the others when the process leads to a known Fourier transform.


