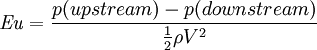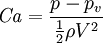To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Euler number (physics)
Product highlightThe Euler number is a dimensionless number used in fluid flow calculations. It expresses the relationship between a local pressure drop over e.g. a restriction and the kinetic energy per volume, and is used to characterize losses in the flow. It is defined as where
Somewhat the same structure, but with a different meaning is the Cavitation number: The Cavitation number is a dimensionless number used in flow calculations. It expresses the relationship between the difference of a local absolute pressure from the vapor pressure and the kinetic energy per volume, and is used to characterize the potential of the flow to cavitate. It is defined as where
See also
References
|
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Euler_number_(physics)". A list of authors is available in Wikipedia. |