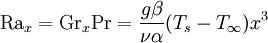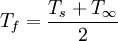Rayleigh number

In fluid mechanics, the Rayleigh number for a fluid is a dimensionless number associated with the heat transfer within the fluid. When the Rayleigh number is below the critical value for that fluid, heat transfer is primarily in the form of conduction; when it exceeds the critical value, heat transfer is primarily in the form of convection.

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

Daily Visual Balance Check

Daily Sensitivity Test

The Rayleigh number is named after Lord Rayleigh and is defined as the product of the Grashof number, which describes the relationship between buoyancy and viscosity within a fluid, and the Prandtl number, which describes the relationship between momentum diffusivity and thermal diffusivity.

For free convection (aka natural convection) near a vertical wall, this number is

where

• Ra_x = Rayleigh number
• Gr_x = Grashof number
• Pr = Prandtl number
• g = acceleration due to gravity
• x = Characteristic length (in this case, the distance from the leading edge)
• T_s = Surface temperature (temperature of the wall)
• T_∞ = Quiescent temperature (fluid temperature far from the surface of the object)
• ν = Kinematic viscosity
• α = Thermal diffusivity
• β = Thermal expansion coefficient

In the above, the fluid properties Pr, ν, α and β are evaluated at the film temperature, which is defined as

For most engineering purposes, the Rayleigh number is large, somewhere around 10⁶ and 10⁸.

In geophysics the Rayleigh number is of fundamental importance: it indicates the presence and strength of convection within a fluid body such as the Earth's mantle, which is a solid but which behaves as a fluid over geological time scales. The high value for the Earth's mantle indicates that convection within the Earth is vigorous and time-varying, and that convection is responsible for almost all the heat transported from the deep interior to the surface.

See also

• Grashof number
• Prandtl number
• Reynolds number
• Péclet number
• Nusselt number