To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Coefficient of thermal expansion
During heat transfer, the energy that is stored in the intermolecular bonds between atoms changes. When the stored energy increases, so does the length of the molecular bond. As a result, solids typically* expand in response to heating and contract on cooling; this response to temperature change is expressed as its coefficient of thermal expansion: The coefficient of thermal expansion is used:
These characteristics are closely related. The volumetric thermal expansion coefficient can be measured for all substances of condensed matter (liquids and solid state). The linear thermal expansion can only be measured in the solid state and is common in engineering applications. * Some substances have a negative expansion coefficient, and will expand when cooled (e.g. freezing water). Product highlight
Thermal expansion coefficientThe thermal expansion coefficient is a thermodynamic property of a substance given by Incropera & DeWitt[1] (p. 537). It relates the change in temperature to the change in a material's linear dimensions. It is the fractional change in length per degree of temperature change. where Linear thermal expansionThe linear thermal expansion is the one-dimensional length change with temperature. Area thermal expansionThe change in area with temperature can be written: For exactly isotropic materials, the area thermal expansion coefficient is very closely approximated as twice the linear coefficient.
Volumetric thermal expansionThe change in volume with temperature can be written[2]:
The volumetric thermal expansion coefficient can be written where Proof: where
Proof:
Note that this equation contains the main term, Thermal expansion coefficients for some common materialsThe expansion and contraction of material must be considered when designing large structures, when using tape or chain to measure distances for land surveys, when designing molds for casting hot material, and in other engineering applications when large changes in dimension due to temperature are expected. The range for α is from 10-7 for hard solids to 10-3 for organic liquids. α varies with the temperature and some materials have a very high variation. Some values for common materials, given in parts per million per Celsius degree: (NOTE: This can also be in kelvins as the changes in temperature are a 1:1 ratio)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Coefficient_of_thermal_expansion". A list of authors is available in Wikipedia. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


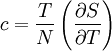
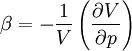
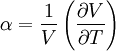



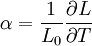
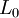 is the original length,
is the original length, 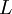 the new length, and
the new length, and 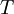 the temperature.
the temperature.
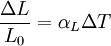
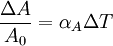
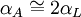
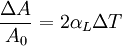
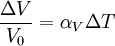
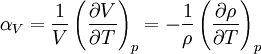
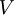 is the volume,
is the volume, 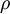 is the density, derivatives are taken at constant pressure
is the density, derivatives are taken at constant pressure 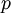 ;
; 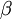 measures the fractional change in density as temperature increases at constant pressure.
measures the fractional change in density as temperature increases at constant pressure.
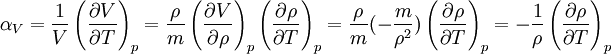
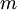 is the mass.
is the mass.
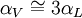
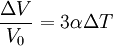
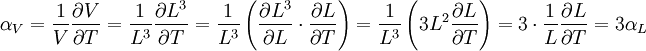
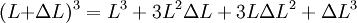
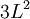 , but also shows a secondary term that scales as
, but also shows a secondary term that scales as 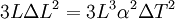 , which shows that a large change in temperature can overshadow a small value for the linear coefficient of thermal expansion. Although the coefficient of linear thermal expansion can be quite small, when combined with a large change in temperature the differential change in length can become large enough that this factor needs to be considered. The last term,
, which shows that a large change in temperature can overshadow a small value for the linear coefficient of thermal expansion. Although the coefficient of linear thermal expansion can be quite small, when combined with a large change in temperature the differential change in length can become large enough that this factor needs to be considered. The last term, 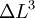 is vanishingly small, and is almost universally ignored.
In anisotropic materials the total volumetric expansion is distributed unequally among the three axes.
is vanishingly small, and is almost universally ignored.
In anisotropic materials the total volumetric expansion is distributed unequally among the three axes.


