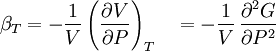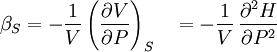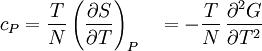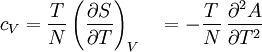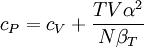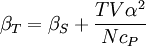To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Material properties (thermodynamics)The thermodynamic properties of materials are intensive thermodynamic parameters which are specific to a given material. Each is directly related to a second order differential of a thermodynamic potential. Examples for a simple 1-component system are:
Product highlightwhere P is pressure, V is volume, T is temperature, S is entropy, and N is the number of particles. For a single component system, only three second derivatives are needed in order to derive all others, and so only three material properties are needed to derive all others. For a single component system, the "standard" three parameters are the isothermal compressibility βT, the specific heat at constant pressure cP, and the coefficient of thermal expansion α. For example, the following equations are true: The three "standard" properties are in fact the three possible second derivatives of the Gibbs free energy with respect to temperature and pressure. ReferencesCallen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics, 2nd Ed., New York: John Wiley & Sons. ISBN 0-471-86256-8.
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Material_properties_(thermodynamics)". A list of authors is available in Wikipedia. |