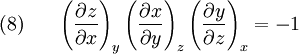To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Exact differentialIn mathematics, a differential dQ is said to be exact, as contrasted with an inexact differential, if the differentiable function Q exists. However, if dQ is arbitrarily chosen, a corresponding Q might not exist. Product highlight
OverviewIn one dimension, a differential is always exact. In two dimensions, in order that a differential be an exact differential in a simply-connected region R of the xy-plane, it is necessary and sufficient that between A and B there exists the relation: In three dimensions, a differential is an exact differential in a simply-connected region R of the xyz-coordinate system if between the functions A, B and C there exist the relations:
These conditions, which are easy to generalize, arise from the independence of the order of differentiations in the calculation of the second derivatives. So, in order for a differential dQ, that is a function of four variables to be an exact differential, there are six conditions to satisfy. In summary, when a differential dQ is exact:
In thermodynamics, when dQ is exact, the function Q is a state function of the system. The thermodynamic functions U, S, H, A and G are state functions. Generally, neither work nor heat is a state function. An exact differential is sometimes also called a 'total differential', or a 'full differential', or, in the study of differential geometry, it is termed an exact form. Partial Differential RelationsFor three variables, x, y and z bound by some differentiable function F(x,y,z), the following total differentials exist[1]
Substituting the first equation into the second and rearranging, we obtain[1]
Since y and z are independent variables, dy and dz may be chosen without restriction. For this last equation to hold in general, the bracketed terms must be equal to zero.[1] Reciprocity RelationSetting the first term in brackets equal to zero yields[1]
A slight rearrangement gives a reciprocity relation,[1]
There are two more permutations of the foregoing derivation that give a total of three reciprocity relations between x, y and z. Reciprocity relations show that the inverse of a partial derivative is equal to its reciprocal. Cyclic RelationSetting the second term in brackets equal to zero yields[1]
Using a reciprocity relation for
If, instead, a reciprocity relation for
Some useful equations derived from exact differentials in two dimensions(See also Bridgman's thermodynamic equations for the use of exact differentials in the theory of thermodynamic equations) Suppose we have five state functions z,x,y,u, and v. Suppose that the state space is two dimensional and any of the five quantites are exact differentials. Then by the chain rule
but also by the chain rule:
and
so that:
which implies that:
Letting v = y gives:
Letting u = y, v = z gives:
using (
See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Exact_differential". A list of authors is available in Wikipedia. |





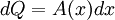
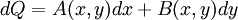
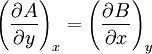
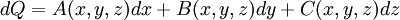
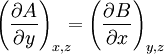 ;
; 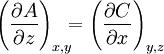 ;
; 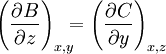
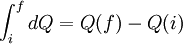 , independent of the path followed.
, independent of the path followed.
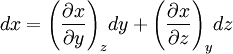
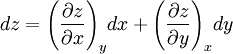 .
.
![d z = {\left ( \frac{\partial z}{\partial x} \right )}_y \left [ {\left ( \frac{\partial x}{\partial y} \right )}_z d y + {\left ( \frac{\partial x}{\partial z} \right )}_y dz \right ] + {\left ( \frac{\partial z}{\partial y} \right )}_x dy](images/math/5/2/c/52c67ba0dc0e3e7fdfc6879c5ed0170e.png) ,
,
![d z = \left [ {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial y} \right )}_z + {\left ( \frac{\partial z}{\partial y} \right )}_x \right ] d y + {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial z} \right )}_y dz](images/math/4/3/3/4336933c06624ec3f8b22470046eec2b.png) ,
,
![\left [ 1 - {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial z} \right )}_y \right ] dz = \left [ {\left ( \frac{\partial z}{\partial x} \right )}_y {\left ( \frac{\partial x}{\partial y} \right )}_z + {\left ( \frac{\partial z}{\partial y} \right )}_x \right ] d y](images/math/e/3/9/e39cc3e51cf0a0a942d2b23be1e61ea2.png) .
.
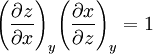 .
.
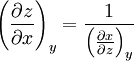 .
.
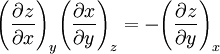 .
.
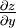 on this equation and reordering gives a cyclic relation (the
on this equation and reordering gives a cyclic relation (the 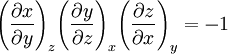 .
.
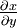 is used with subsequent rearrangement, a standard form for implicit differentiation is obtained:
is used with subsequent rearrangement, a standard form for implicit differentiation is obtained:
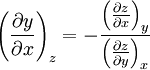 .
.
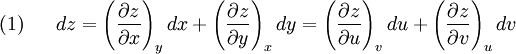
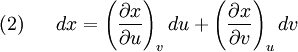
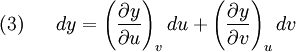
![(4)~~~~~ dz = \left[ \left(\frac{\partial z}{\partial x}\right)_y \left(\frac{\partial x}{\partial u}\right)_v + \left(\frac{\partial z}{\partial y}\right)_x \left(\frac{\partial y}{\partial u}\right)_v \right]du](images/math/e/b/4/eb4403091698adde7d61fa6caed95c8c.png)
![+ \left[ \left(\frac{\partial z}{\partial x}\right)_y \left(\frac{\partial x}{\partial v}\right)_u + \left(\frac{\partial z}{\partial y}\right)_x \left(\frac{\partial y}{\partial v}\right)_u \right]dv](images/math/0/5/0/0502fc18d6b162fda0d70f94a537a388.png)
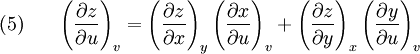
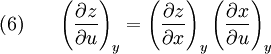
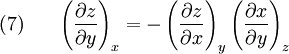
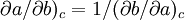 gives the
gives the