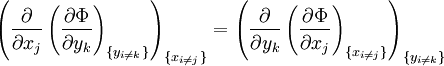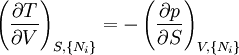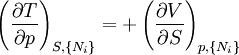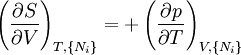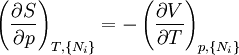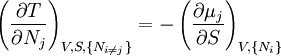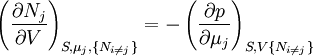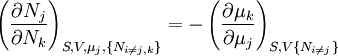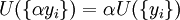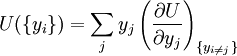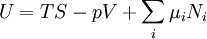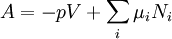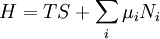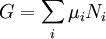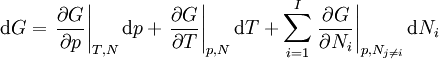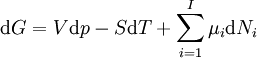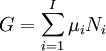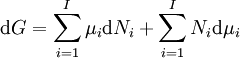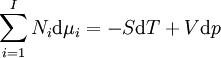To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Thermodynamic potential
A thermodynamic potential is a scalar potential function used to represent the thermodynamic state of a system. One main thermodynamic potential which has a physical interpretation is the internal energy, U. It is the energy of configuration of a given system of conservative forces (that is why it is a potential) and only has meaning with respect to a defined set of references (or datums). Expressions for all other thermodynamic energy potentials are derivable via Legendre transforms from an expression for U. In thermodynamics, certain forces, such as gravity, are typically disregarded when formulating expressions for potentials. For example, while all the working fluid in a steam engine may have higher energy due to gravity while sitting on top of Mt. Everest than it would at the bottom of the Mariana trench, the gravitational potential energy term in the formula for the internal energy would usually be ignored because changes in gravitational potential within the engine during operation would be negligible. Five common thermodynamic energy potentials are:
where T = temperature, S = entropy, p = pressure, V = volume. The Helmholtz free energy is often denoted by the symbol F, but the use of A is preferred by IUPAC (See Alberty, 2001). Ni is the number of particles of type i in the system. For the sake of completeness, the set of all Ni are also included as natural variables, although they are sometimes ignored. These five common potentials are all energy potentials, but there are also entropy potentials. Product highlight
Description and interpretationThermodynamic potentials are very useful when calculating the equilibrium results of a chemical reaction, or when measuring the properties of materials in a chemical reaction. The chemical reactions usually take place under some simple constraints such as constant pressure and temperature, or constant entropy and volume, and when this is true, there is a corresponding thermodynamic potential which comes into play. Just as in mechanics, the system will tend towards lower values of potential and at equilibrium, under these constraints, the potential will take on an unchanging minimum value. The thermodynamic potentials can also be used to estimate the total amount of energy available from a thermodynamic system under the appropriate constraint. In particular: (see principle of minimum energy for a derivation)
Natural variablesThe variables that are held constant in this process are termed the natural variables of that potential. The natural variables are important not only for the above mentioned reason, but also because if a thermodynamic potential can be determined as a function of its natural variables, all of the thermodynamic properties of the system can be found by taking partial derivatives of that potential with respect to its natural variables and this is true for no other combination of variables. Conversely, if a thermodynamic potential is not given as a function of its natural variables, it will not, in general, yield all of the thermodynamic properties of the system. Conjugate variablesJust as a small increment of energy in a mechanical system is the product of a force times a small displacement, so an increment in the energy of a thermodynamic system can be expressed as the sum of the products of certain generalized "forces" which, when unbalanced, cause certain generalized "displacements" to occur, with their product being the energy transferred as a result. These forces and their associated displacements are called conjugate variables. For example, consider the pV conjugate pair. The pressure P acts as a generalized force: Pressure differences force a change in volume dV, and their product is the energy lost by the system due to work. Here pressure is the driving force, volume is the associated displacement, and the two form a pair of conjugate variables. In a similar way, temperature differences drive changes in entropy, and their product is the energy transferred by heat transfer. The thermodynamic force is always an intensive variable and the displacement is always an extensive variable, yielding an extensive energy. The intensive (force) variable is the derivative of the internal energy with respect to the extensive (displacement) variable, with all other extensive variables held constant. More conjugate variables - the chemical potentialThe theory of thermodynamic potentials is not complete until we consider the number of particles in a system as a variable on par with the other extensive quantities such as volume and entropy. The number of particles is, like volume and entropy, the displacement variable in a conjugate pair. The generalized force component of this pair is the chemical potential. The chemical potential may be thought of as a force which, when imbalanced, pushes an exchange of particles, either with the surroundings, or between phases inside the system. In cases where there are a mixture of chemicals and phases, this is a useful concept. For example if a container holds liquid water and water vapor, there will be a chemical potential (which is negative) for the liquid which pushes the water molecules into the vapor (evaporation) and a chemical potential for the vapor, pushing vapor molecules into the liquid (condensation). Only when these "forces" equilibrate and the chemical potentials of each phase is equal, is equilibrium obtained. More thermodynamic potentialsNotice that the set of natural variables for the above four potentials are formed from every combination of the T-S and P-V variables, as long as two conjugate variables are not used. There is no reason to ignore the μi − Ni conjugate pairs, and in fact we may define four additional potentials for each species. Using IUPAC notation in which the brackets contain the natural variables (other than the main four), we have:
If there is only one species, then we are done, but if there are, say two species, then there will be additional potentials such as U[μ1,μ2] = U − μ1N1 − μ2N2 and so on. If there are D dimensions to the thermodynamic space, then there are 2D unique thermodynamic potentials. For the most simple case, a single phase ideal gas, there will be three dimensions, yielding eight thermodynamic potentials. In statistical mechanics, the relationship between the Helmholtz free energy and the partition function is fundamental, and is used to calculate the thermodynamic properties of matters; see configuration integral for more details. The fundamental equationsThe definitions of the thermodynamic potentials may be differentiated and, along with the first and second law of thermodynamics, a set of differential equations known as the fundamental equations may be derived. By the first law of thermodynamics, any differential change in the internal energy U of a system can be written as the sum of heat flowing into the system and work done by the system on the environment, along with any change due to the addition of new particles to the system: where δQ is the infinitesimal heat flow into the system, and δW is the infinitesimal work done by the system, μi is the chemical potential of particle type i and Ni is the number of type i particles. (Note that neither δQ nor δW are exact differentials. Small changes in these variables are therefore represented with δ rather than d.) By the second law of thermodynamics, we can express the internal energy change in terms of state functions and their differentials: where T is temperature, S is entropy, p is pressure, and V is volume, and the equality holds for reversible processes. This leads to the standard differential form of the internal energy: Applying Legendre transforms repeatedly, the following differential relations hold for the four potentials:
Note that the infinitesimals on the right hand side of each of the above equations are of the natural variables of the potential on the left hand side. The above relations illustrate that when the natural variables of each potential are held constant, the potential decreases in value in an irreversible way, approaching its constant, minimum value at equilibrium. Similar equations can be developed for all of the other thermodynamic potentials of the system. There will be one fundamental equation for each thermodynamic potential, resulting in a total of 2D fundamental equations. The equations of stateWe can use the above equations to derive some differential definitions of some thermodynamic parameters. If we define Φ to stand for any of the thermodynamic potentials, then the above equations are of the form: where xi and yi are conjugate pairs, and the yi are the natural variables of the potential Φ. From the chain rule it follows that: Where where, in the last equation, φ is any of the thermodynamic potentials U, A, H, G and and so on. In all, there will be D equations for each potential resulting in a total of D 2D equations of state. If the D equations of state for a particular potential are known, then the fundamental equation for that potential can be determined. This means that all thermodynamic information about the system will be known, and that the fundamental equations for any other potential can be found, along with the corresponding equations of state. The Maxwell relationsAgain, define xi and yi to be conjugate pairs, and the yi to be the natural variables of some potential Φ. We may take the "cross differentials" of the state equations, which obey the following relationship: From these we get the Maxwell relations. There will be (D-1)/2 of them for each potential giving a total of D(D-1)/2 equations in all. If we restrict ourselves the U, A, H, G Using the equations of state involving the chemical potential we get equations such as: and using the other potentials we can get equations such as: Euler integralsAgain, define xi and yi to be conjugate pairs, and the yi to be the natural variables of the internal energy. Since all of the natural variables of the internal energy U are extensive quantities it follows from Euler's homogeneous function theorem that the internal energy can be written as: From the equations of state, we then have: Substituting into the expressions for the other main potentials we have: As in the above sections, this process can be carried out on all of the other thermodynamic potentials. Note that the Euler integrals are sometimes also referred to as fundamental equations. The Gibbs-Duhem relationDeriving the Gibbs-Duhem equation from basic thermodynamic state equations is straightforward[1]. The Gibbs free energy With the substitution of two of the Maxwell relations and the definition of chemical potential, this is transformed into: The chemical potential is just another name for the partial molar Gibbs free energy, and as such: Subtracting yields the Gibbs-Duhem relation: The Gibbs-Duhem is a relationship among the intensive parameters of the system. It follows that for a simple system with I components, there will be I + 1 independent parameters, or degrees of freedom. For example, a simple system with a single component will have two degrees of freedom, and may be specified by only two parameters, such as pressure and volume for example. The law is named after Josiah Gibbs and Pierre Duhem. Chemical reactionsChanges in these quantities are useful for assessing the degree to which a chemical reaction will proceed. The relevant quantity depends on the reaction conditions, as shown in the following table. Δ denotes the change in the potential and at equilibrium the change will be zero.
Most commonly one considers reactions at constant p and T, so the Gibbs free energy is the most useful potential in studies of chemical reactions.
References
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Thermodynamic_potential". A list of authors is available in Wikipedia. |


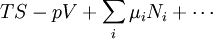
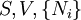
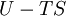
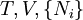
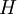
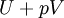
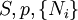
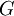
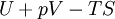
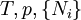
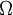
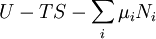
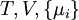



![U[\mu_j]=U-\mu_jN_j\,](images/math/2/6/9/269912f4aa53f453130defff4762ac97.png)
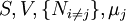
![A[\mu_j]=U-TS-\mu_jN_j\,](images/math/f/b/f/fbf99160142ff7ad27d5bc26816c2fdb.png)
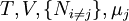
![H[\mu_j]=U+pV-\mu_jN_j\,](images/math/4/9/0/490ddd5ef91f255a4acf049d99b48e24.png)
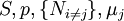
![G[\mu_j]=U+pV-TS-\mu_jN_j\,](images/math/2/a/b/2abfd370faa7bb1e364a14fb58c493f3.png)
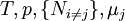
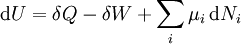
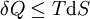
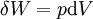
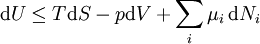
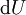
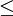
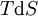

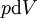
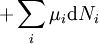
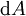
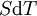
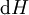
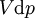
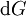
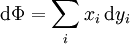
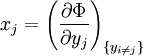
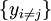 is the set of all natural variables of
is the set of all natural variables of 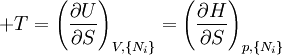
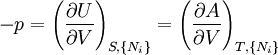
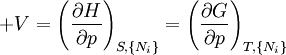
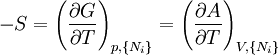
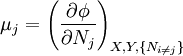
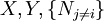 are the set of natural variables for that potential, excluding
are the set of natural variables for that potential, excluding ![-N_j=\left(\frac{\partial U[\mu_j]}{\partial \mu_j}\right)_{S,V,\{N_{i\ne j}\}}](images/math/3/c/1/3c18bf0022d4ea560cad992fb8ec60e5.png)