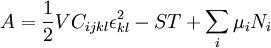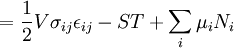To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Helmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential which measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature. For such a system, the negative of the difference in the Helmholtz energy is equal to the maximum amount of work extractable from a thermodynamic process in which temperature is held constant. Under these conditions, it is minimized at equilibrium. The Helmholtz free energy was developed by Hermann von Helmholtz and is denoted by the letter A (from the German “Arbeit” or work), or the letter F . The IUPAC recommends the letter A as well as the use of name Helmholtz energy;[1] in physics, A is called the Helmholtz function or simply “free energy”. While Gibbs free energy is most commonly used as a measure of thermodynamic potential, especially in the field of chemistry, the isobaric restriction on that quantity is sometimes inconvenient. For example, in explosives research, Helmholtz free energy is often used since explosive reactions by their nature induce pressure changes. Product highlight
DefinitionThe Helmholtz energy is defined as: where
Mathematical developmentFrom the first law of thermodynamics we have: where U is the internal energy, δQ is the energy added by heating and δW = pdV is the work done by the system. From the second law of thermodynamics, for a reversible process we may say that δQ = TdS. Differentiating the expression for A we have: For a process which is not reversible, the energy will be smaller than its equilibrium value so we may say that, in general, It is seen that if a thermodynamic process is isothermal (i.e. occurs at constant temperature), then dT = 0 and thus The negative of the change in the Helmholtz energy is the maximum work attainable from the system in an isothermal process. In more mathematical terms, the integral of − dA over any isotherm in state space is the maximum work attainable from the system. If, in addition the volume is held constant as well, the above equation becomes: with the equality holding at equilibrium. It is seen that the Helmholtz energy for a general system in which the temperature and volume are held constant will continuously decrease to its minimum value, which it maintains at equilibrium. In a more general form, the first law describes the internal energy with additional terms involving the chemical potential and the number of particles of various types. The differential statement for dA is then: where μi is the chemical potential for an i-type particle, and Ni is the number of such particles. With this definition, we may say that the negative of the Helmholtz energy is the maximum amount of work energy available from a system in which the initial and final states have the same temperature and number of particles. Further generalizations will add even more terms whose extensive differential term must be set to zero in order for the interpretation of the Helmholtz energy to hold. In statistical mechanics, the relationship between the Helmholtz free energy and the partition function is fundamental, and is used to calculate the thermodynamic properties of matters; see configuration integral for more details. Generalized Helmholtz energyIn the more general case, the mechanical term (pdV) must be replaced by the product of the volume times the stress times an infinitesimal strain:[3] where σij is the stress tensor, and
where we are now using Einstein notation for the tensors, in which repeated indices in a product are summed. We may integrate the expression for dA to obtain the Helmholtz energy: See also
References
Further reading
|
|||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Helmholtz_free_energy". A list of authors is available in Wikipedia. | |||||||||||||





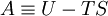
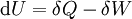
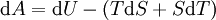
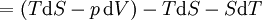
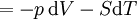
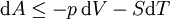
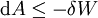
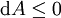
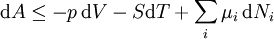
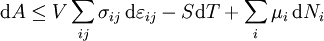
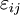 is the strain tensor. In the case of linear
is the strain tensor. In the case of linear