To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Stress (physics)
Stress, defined as force per unit area, is a measure of the intensity of the total internal forces acting within a body across imaginary internal surfaces, as a reaction to external applied forces and body forces. It was introduced into the theory of elasticity by Cauchy around 1822. Stress is a concept that is based on the concept of continuum. Stress is often broken down into its shear and normal components as these have unique physical significance. In short, stress is to force as strain is to deformation. The term normal stress in rheology is called extensional stress and in acoustics is called longitudinal stress. Solids, liquids and gases have stress fields. Static fluids support normal stress (hydrostatic pressure) but will flow under shear stress. Moving viscous fluids can support shear stress (dynamic pressure). Solids can support both shear and normal stress, with ductile materials failing under shear and brittle materials failing under normal stress. All materials have temperature dependent variations in stress related properties, and non-newtonian materials have rate-dependent variations. Product highlight
Stress tensorStress is a second-order tensor with nine components, but can be fully described with six components due to symmetry in the absence of body moments. In N dimensions, the stress tensor where the dFi are the components of the resultant force vector acting on a small area dA which can be represented by a vector dAj perpendicular to the area element, facing outwards and with length equal to the area of the element. In elementary mechanics, the subscripts are often denoted x, y, z rather than 1,2,3.
The components When the stress tensor is needed to fully describe the state of stress in a body, it is useful to break the concept up into smaller parts that have physical significance. In a 1-dimensional system, such as a uniaxially loaded bar, stress is simply equal to the applied force divided by the cross-sectional area of the bar (see also pressure). The 2-D or 3-D cases are more complex. In three dimensions, the internal force acting on a small area dA of a plane that passes through a point P can be resolved into three components: one normal to the plane and two parallel to the plane (see Figure 1). The normal component divided by dA gives the normal stress (usually denoted σ), and the parallel components divided by the area dA give shear stresses (denoted τ or τ in elementary textbooks). If the area dA is finite then, strictly, these are average stresses. In the limit when dA approaches zero, the stresses become stresses at the point P. In general, stress varies from point to point and so is a tensor field. Stress in one-dimensional bodiesAll real objects occupy three-dimensional space. However, if two dimensions are very large or very small compared to the others, the object may be modelled as one-dimensional. This simplifies the mathematical modelling of the object. One-dimensional objects include a piece of wire loaded at the ends and viewed from the side, and a metal sheet loaded on the face and viewed up close and through the cross section. For one-dimensional objects, the stress tensor has only one component and is indistinguishable from a scalar. The simplest definition of stress, σ = F/A, where A is the initial cross-sectional area prior to the application of the load, is called engineering stress or nominal stress. However, when any material is stretched, its cross-sectional area may change by an amount that depends on the Poisson's ratio of the material. Engineering stress neglects this change in area. The stress axis on a stress-strain graph is often engineering stress, even though the sample may undergo a substantial change in cross-sectional area during testing. True stress is an alternative definition in which the initial area is replaced by the current area. In engineering applications, the initial area is always known, and so calculations using nominal stress are generally easier. For small deformation, such as in practical material usage, the reduction in cross-sectional area is small and the distinction between nominal and true stress is insignificant; so the change of cross-sectional area could be assumed to be a constant value. This is not so for the large deformations typical of elastomers and plastic materials when the change in cross-sectional areas can be significant. In one dimension, conversion between true stress and nominal (engineering) stress is given by
where εe is nominal (engineering) strain, and σe is nominal (engineering) stress. The relationship between true strain and engineering strain is given by
In uniaxial tension, true stress is then greater than nominal stress. The converse holds in compression. Example: A steel bolt of diameter 5 mm has a cross-sectional area of 19.6 mm2. A load of 50 N induces a stress (force distributed over the cross section) of σ = 50/19.6 = 2.55 MPa (N/mm2). This can be thought of as each square millimeter of the bolt supporting 2.55 N of the total load. In another bolt with half the diameter, and hence a quarter the cross-sectional area, carrying the same 50 N load, the stress will be quadrupled (10.2 MPa). The ultimate tensile strength is a property of a material and is usually determined experimentally from a uniaxial tensile test. It allows the calculation of the load that would cause fracture. The compressive strength is a similar property for compressive loads. The yield strength is the value of stress causing plastic deformation. Stress in two-dimensional bodiesAll real objects occupy 3-dimensional space. However, if one dimension is very large or very small compared to the others, the object may be modelled as two-dimensional. This simplifies the mathematical modelling of the object. Two-dimensional objects include a piece of wire loaded on the sides and viewed up close and through the cross-section and a metal sheet loaded in-plane and viewed face-on. Notice that the same physical, three-dimensional object can be modelled as one-dimensional, two-dimensional or even three-dimensional, depending on the loading and viewpoint of the observer. Plane stressPlane stress is a two-dimensional state of stress (Figure 2). This 2-D state models well the state of stresses in a flat, thin plate loaded in the plane of the plate. Figure 2 shows the stresses on the x- and y-faces of a differential element. Not shown in the figure are the stresses in the opposite faces and the external forces acting on the material. Since moment equilibrium of the differential element shows that the shear stresses on the perpendicular faces are equal, the 2-D state of stresses is characterized by three independent stress components (σx, σy, τxy). Note that forces perpendicular to the plane can be abbreviated. For example, σx is an abbreviation for σxx. This notation is described further below. See also plane strain. Principal stresses in 2-DAugustin Louis Cauchy was the first to demonstrate that at a given point, it is always possible to locate two orthogonal planes in which the shear stress vanishes. These planes in which the normal forces are acting are called the principal planes, while the normal stresses on these planes are the principal stresses. They are the eigenvalues of the stress tensor and are orthogonal because the stress tensor is symmetric (as per the spectral theorem). Eigenvalues are invariants with respect to choice of basis and are the roots of the Cayley–Hamilton theorem (although the term 'the' invariants usually means (I1,I2,I3)). Mohr's circle is a graphical method of extracting the principal stresses in a 2-dimensional stress state. The maximum and minimum principal stresses are the maximum and minimum possible values of the normal stresses. The maximum principal stress controls brittle fracture. The two dimensional Cauchy stress tensor is defined as: Then principal stresses σ1,σ2 are equal to: Those formulas have geometrical interpretation in the form of Mohr Circle presented in section below. Mohr's circleMohr's circle is a graphical representation of any 2-D stress state. It was named for Christian Otto Mohr. Mohr's circle may also be applied to three-dimensional stress. In this case, the diagram has three circles, two within a third. Mohr's circle is used to find the principal stresses, maximum shear stresses, and principal planes. For example, if the material is brittle, the engineer might use Mohr's circle to find the maximum component of normal stress (tension or compression); and for ductile materials, the engineer might look for the maximum shear stress. Stress in three dimensional bodiesCauchy's principleCauchy enunciated the principle that, within a body, the forces that an enclosed volume imposes on the remainder of the material must be in equilibrium with the forces upon it from the remainder of the body. This intuition provides a route to characterizing and calculating complicated patterns of stress. To be exact, the stress at a point may be determined by considering a small element of the body that has an area ΔA, over which a force ΔF acts. By making the element infinitesimally small, the stress vector σ is defined as the limit: Being a tensor, the stress has two directional components: one for force and one for plane orientation; in three dimensions these can be two forces within the plane of the area A, the shear components, and one force perpendicular to A, the normal component. Therefore the shear stress can be further decomposed into two orthogonal force components within the plane. This gives rise to three total stress components acting on this plane. For example in a plane orthogonal to the x axis, there can be a normal force applied in the x direction and a combination of y and z in plane force components. The considerations above can be generalized to three dimensions. However, this is very complicated, since each shear loading produces shear stresses in one orientation and normal stresses in other orientations, and vice versa. Often, only certain components of stress will be important, depending on the material in question. The von Mises stress is derived from the distortion energy theory and is a simple way to combine stresses in three dimensions to calculate failure criteria of ductile materials. In this way, the strength of material in a 3-D state of stress can be compared to a test sample that was loaded in one dimension. The stress tensor in 3-D(see also viscosity and Hooke's law for development of the stress tensor in viscous and elastic materials respectively) Because the behavior of a body does not depend on the coordinate systems used to measure it, stress can be described by a tensor. In the absence of body moments, the stress tensor is symmetric and can always be resolved into the sum of two symmetric tensors:
In the case of a fluid, Pascal's law shows that the hydrostatic stress is the same in all directions, at least to a first approximation, so can be captured by the scalar quantity pressure.
Thus, in the case of a solid, the hydrostatic (or isostatic) pressure For viscous fluids the Cauchy stress tensor σ is defined as:
If the fluid is incompressible it follows that: If the fluid is compressible the assumption above is true, if the viscosity of compression Principal stresses in 3-DThe three dimensional Cauchy stress tensor is defined as: In equilibrium, τyx = τxy, τzx = τxz, and τzy = τyz, so the matrix is effectually symmetric. If not in equilibrium, other methods - not outlined here - must be used to make it symmetric before calculations can begin. To calculate the principal stresses σ1,σ2 and σ3 the three invariants of the Cauchy stress tensor must be calculated: Then the characteristic equation of 3-D principal stresses is expressed as: The three roots of this equation are principal stresses σ1,σ2 and σ3. When they are found it can be shown that the three invariants can be expressed in terms of principal stresses: Generalized notationIn the generalized stress tensor notation, the tensor components are written σij, where i and j are in {1;2;3}. (caution: subscript notation in this section is different from the rest of the article - the order of subscripts is reversed) The first step is to number the sides of the cube.
When the lines are parallel to a vector base
σij is then the component along the i axis that applies on the j side of the cube. (Or in books in the English language, σij is the stress on the i face acting in the j direction -- the transpose of the subscript notation herein. But transposing the subscript notation produces the same stress tensor, since a symmetric matrix is equal to its transpose.)
This generalized notation allows an easy writing of equations of the continuum mechanics, such as the generalized Hooke's law: The correspondence with the former notation is thus:
Why is Newtonian stress a symmetric tensor?The fact that the Newtonian stress is a symmetric tensor follows from some simple considerations. The force on a small volume element will be the sum of all the stress forces over the surface area of that element. Suppose we have a volume element in the form of a long bar with a triangular cross section, where the triangle is a right triangle. We can neglect the forces on the ends of the bar, because they are small compared to the faces of the bar. Let Let's say The total force on the volume element will be: Let's suppose that the volume element contains mass, at a constant density. The important point is that if we make the volume smaller, say by halving all lengths, the area will decrease by a factor of four, while the volume will decrease by a factor of eight. As the size of the volume element goes to zero, the ratio of area to volume will become infinite. The total stress force on the element is proportional to its area, and so as the volume of the element goes to zero, the force/mass (i.e. acceleration) will also become infinite, unless the total force is zero. In other words: This, along with the second equation above, proves that the σ function is a linear vector operator (i.e. a tensor). By an entirely analogous argument, we can show that the total torque on the volume element (due to stress forces) must be zero, and that it follows from this restriction that the stress tensor must be symmetric. However, there are two fundamental ways in which this mode of thinking can be misleading. First, when applying this argument in tandem with the underlying assumption from continuum mechanics that the Knudsen number is strictly less than one, then in the limit Equilibrium conditionsThe state of stress as defined by the stress tensor is an equilibrium state if the following conditions are satisfied: σij are the components of the tensor, and f 1 , f 2 , and f 3 are the body forces (force per unit volume). These equations can be compactly written using Einstein notation in which repeated indices are summed. Defining The equilibrium conditions may be derived from the condition that the net force on an infinitesimal volume element must be zero. Consider an infinitesimal cube aligned with the x1, x2, and x3 axes, with one corner at xi and the opposite corner at xi + dxi and having each face of area dA. Consider just the faces of the cube which are perpendicular to the x1 axis. The area vector for the near face is [ − dA,0,0] and for the far face it is [dA,0,0]. The net stress force on these two opposite faces is A similar calculation can be carried out for the other pairs of faces. The sum of all the stress forces on the infinitesimal cube will then be Since the net force on the cube must be zero, it follows that this stress force must be balanced by the force per unit volume fi on the cube (e.g., due to gravitation, electromagnetic forces, etc.) which yields the equilibrium conditions written above. Equilibrium also requires that the resultant moment on the cube of material must be zero. Taking the moment of the forces above about any suitable point, it follows that, for equilibrium in the absence of body moments
The stress tensor is then symmetric and the subscripts can be written in either order. Stress in big bending deformationFor big deformations in of the body, the stress in the cross-section is calculated using an extended version of this formula. First the following assumptions must be made:
The big bending is usually assumed when bending radius ρ is smaller than ten section heights h:
With those assumptions the stress in big bending is calculated as: where
When bending radius ρ approaches infinity and y is zero, the original formula is back:
Stress measurementAs with force, stress cannot be measured directly but is usually inferred from measurements of strain and knowledge of elastic properties of the material. Devices capable of measuring stress indirectly in this way are strain gauges and piezoresistors. UnitsThe SI unit for stress is the pascal (symbol Pa), the same as that of pressure. Since the pascal is so small (1 N/m2), engineering quantities are usually measured in megapascals (MPa) or gigapascals (GPa). In US Customary units, stress is expressed in pounds-force per square inch (psi) or kilopounds-force per square inch (ksi). See also pressure. Residual stressResidual stresses are stresses that remain after the original cause of the stresses has been removed. Residual stresses occur for a variety of reasons, including inelastic deformations and heat treatment. Heat from welding may cause localized expansion. When the finished weldment cools, some areas cool and contract more than others, leaving residual stresses. Castings may also have large residual stresses due to uneven cooling. While uncontrolled residual stresses are undesirable, many designs rely on controlled ones. For example, toughened glass and prestressed concrete rely on residual stress to prevent brittle failure. Similarly, a gradient in martensite formation leaves residual stress in some swords with particularly hard edges (notably the katana), which can prevent the opening of edge cracks. In certain types of gun barrels made with two telescoping tubes forced together, the inner tube is compressed while the outer tube stretches, preventing cracks from opening in the rifling when the gun is fired. These tubes are often heated or immersed in liquid nitrogen to aid assembly. In manufacturing, press fits are the most common intentional use of residual stress. Automotive wheel studs, for example, are pressed into holes on the wheel hub. The holes are smaller than the studs, requiring force to drive the studs into place. The residual stresses fasten the parts together. Nails are another example. See also
Books
Categories: Continuum mechanics | Materials science |
||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Stress_(physics)". A list of authors is available in Wikipedia. |





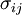 is defined by:
is defined by:
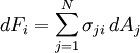
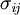 of the stress tensor depend on the orientation of the plane that passes through the point under consideration, i.e on the viewpoint of the observer. This would lead to the incorrect conclusion that the stress on a structure, and hence its proximity to failure, depends on the viewpoint of the observer. However, every tensor, including stress, has invariants that do not depend on the choice of viewpoint. The length of a first-order tensor, i.e a vector, is a simple example. The existence of invariants means that the components seen by one observer are related, via the tensor transformation relations, to those seen by any other observer. The transformation relations for a second-order tensor like stress are different from those of a first-order tensor, which is why it is misleading to speak of the stress 'vector'.
of the stress tensor depend on the orientation of the plane that passes through the point under consideration, i.e on the viewpoint of the observer. This would lead to the incorrect conclusion that the stress on a structure, and hence its proximity to failure, depends on the viewpoint of the observer. However, every tensor, including stress, has invariants that do not depend on the choice of viewpoint. The length of a first-order tensor, i.e a vector, is a simple example. The existence of invariants means that the components seen by one observer are related, via the tensor transformation relations, to those seen by any other observer. The transformation relations for a second-order tensor like stress are different from those of a first-order tensor, which is why it is misleading to speak of the stress 'vector'. ![\sigma_{ij}= \left[{\begin{matrix} {\sigma _x } & {\tau _{xy}} \\ {\tau _{xy}} & {\sigma _y } \\ \end{matrix}}\right].](images/math/8/8/5/885dfa41b9bbd974dca5984a8ff70072.png)
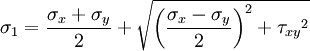
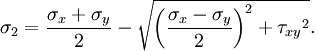
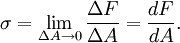
 is defined as one third of the trace of the tensor, i.e., the mean of the diagonal terms.
is defined as one third of the trace of the tensor, i.e., the mean of the diagonal terms.
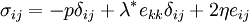
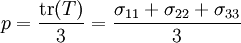
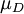 vanishes:
vanishes:
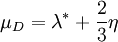
![\sigma_{ij}= \left[{\begin{matrix} {\sigma _x } & {\tau _{xy}} & {\tau _{xz}} \\ {\tau _{yx}} & {\sigma _y } & {\tau _{yz}} \\ {\tau _{zx}} & {\tau _{zy}} & {\sigma _z } \\ \end{matrix}}\right]](images/math/8/3/4/8348f72f98295fed6c95e5736604a9f2.png)
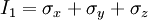
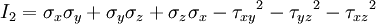
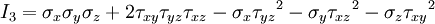
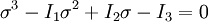
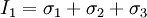
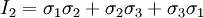
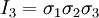
 , then:
, then:
 are called j and -j; and
are called j and -j; and
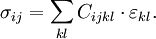
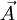 be the vector area of one face of the bar,
be the vector area of one face of the bar, 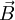 be the area of the other, and
be the area of the other, and 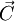 be the area of the "hypotenuse face" of the bar. It can be seen that
be the area of the "hypotenuse face" of the bar. It can be seen that
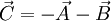
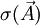 is the force on area
is the force on area 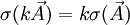
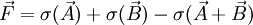
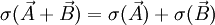
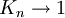 , the symmetry assumptions in the stress tensor may break down. This is the case of
, the symmetry assumptions in the stress tensor may break down. This is the case of 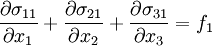
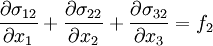
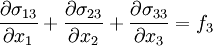
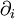 as
as 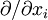 the equilibrium conditions are written:
the equilibrium conditions are written:
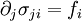
![dF_i=\sigma_{1i}([x_1+dx_1,x_2,x_3])\,dA-\sigma_{1i}([x_1,x_2,x_3])\,dA \approx \partial_1\sigma_{1i}\,dV](images/math/6/9/9/6995f64b061819142fe97b96c4e7d8e4.png)
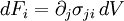
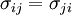 .
.
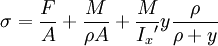
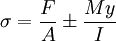 .
.


