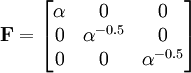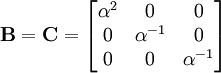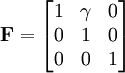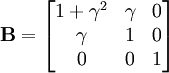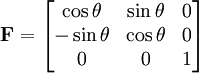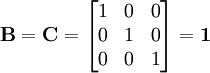To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Finite deformation tensorsIn continuum mechanics, finite deformation tensors are used when the deformation of a body is sufficiently large to invalidate the assumptions inherent in small strain theory. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue. Product highlight
Deformation gradient tensorThe position (vector) of a particle in the initial, undeformed state of a body is denoted The quantity or, in index notation: It is assumed that
Note: The notation and terminology used here was introduced in the "Non-Linear Field Theories of Mechanics” by C.Truesdell and myself (Walter Noll), published in 1965. I invented much of this notation and terminology, but I now realize that some of it is misleading and should be changed. For example “Deformation Gradient” should be replaced by “Transplacement Gradient”. A modern, frame-free and coordinate-free analysis of the mathematical concept of deformation can be found in the first four parts of my "Five Contributions to Natural Philosophy", published in 2005 and available on my website www.math.cmu.edu/~wn0g/noll Polar DecompositionThe deformation gradient
The tensor The spectral decompositions of and where λi are the principal stretches, and The principal directions are related by . Rotation-Independent Deformation MeasuresSince a pure rotation should not induce any stresses in a deformable body, it is often convenient to use rotation-independent measures of the deformation in continuum mechanics. As a rotation followed its inverse rotation leads to no change ( The Right Cauchy-Green deformation tensorThe right Cauchy-Green deformation tensor (named after Augustin Louis Cauchy and George Green) is defined as:: or The spectral decomposition of Physically, the Cauchy-Green tensor gives us the square of local change in distances due to deformation. The Left Cauchy-Green deformation tensorReversing the order of multiplication in the formula for the Finger tensor leads to the left Cauchy-Green deformation tensor which is defined as: In index notation: The spectral decomposition of The Finger deformation tensorThe inverse of the left Cauchy-Green tensor is often called the Finger tensor. This tensor is named after Josef Finger (1894). ExamplesUniaxial extension of an incompressible materialThis the case where a specimen is stretched in 1-direction with a stretch ratio of
Simple shear
Rigid body rotation
See also
References
Categories: Continuum mechanics | Non-Newtonian fluids |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Finite_deformation_tensors". A list of authors is available in Wikipedia. |





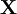 relative to some coordinate basis. The position of the same particle in the deformed state is denoted
relative to some coordinate basis. The position of the same particle in the deformed state is denoted 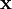 . If
. If 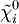 is a line segment joining two nearby particles in the undeformed state and
is a line segment joining two nearby particles in the undeformed state and 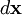 is the line segment joining the same two particles in the defomed state, the linear transformation between the two line segments is given by
is the line segment joining the same two particles in the defomed state, the linear transformation between the two line segments is given by
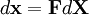
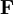 is called the deformation gradient and is given by:
is called the deformation gradient and is given by:
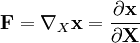
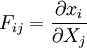
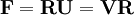
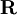 is an proper orthogonal tensor, and
is an proper orthogonal tensor, and 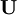 and
and 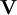 are both positive definite symmetric tensors of second order.
are both positive definite symmetric tensors of second order.
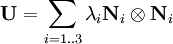
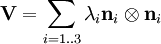
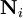 ,
, 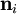 are the directions of the principal stretches (principal directions).
are the directions of the principal stretches (principal directions).
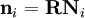
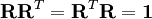 ) we can exclude the rotation by multiplying
) we can exclude the rotation by multiplying 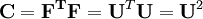
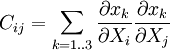
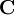 is
is
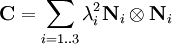
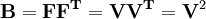
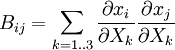
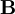 is
is
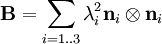
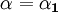 . If the volume remains constant, the contraction in the other two directions is such that
. If the volume remains constant, the contraction in the other two directions is such that 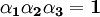 or
or 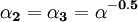 . Then:
. Then: